Sinistar: el arcade de la eterna juventud

No hay nada como encontrar un ejemplo divertido (esto siempre es cuestionable) para apoyarse a la hora explicar uno de tantos áridos conceptos que pueblan la electrónica digital, la computación y el procesamiento de señal. Hace tiempo me topé con un vídeo fantástico publicado por la revista IEEE Spectrum (Five Infamous Arcade-Game Glitches), en el que hablaban de fallos de programación (glitches) en juegos de máquinas recreativas: Asteroids (Atari), Donkey Kong (Nintendo), Sinistar (Williams Electronics), Ms. Pacman (Midway) y Centipede (Atari) .

Me llamó la atención el glitch del juego Sinistar, que me venía de perlas para explicar la aritmética en complemento a 2, fundamental en el mundo de los sistemas digitales. En este juego existía la posibilidad de pasar de tener 1 única vida a disponer de 255. Todo esto debido a un despiste de programación y al funcionamiento de la aritmética binaria (en este caso de 8 bits). Por cierto, matizar que lo que voy a contar es bastante simple, pero divertido.

Primero os explico muy por encima un par de conceptos sobre binario que si ya tenéis experiencia podéis ir directos al meollo pulsando aquí.

Código binario

Primero tenemos que ver qué es el código binario y mi explicación se centrará en el uso del binario para representar números. El binario es un sistema de representación numérica posicional en base 2. Un sistema posicional en base B representa números utilizando dígitos que pueden tomar valores entre el 0 y  B-1 (del 0 al 1 en el caso del binario; del 0 al 9 en el caso del decimal, etc.), y que se escriben uno detrás de otro. La posición i que ocupa cada dígito determina su peso. Si asumimos que el dígito más a la derecha tiene la posición 0 y que el dígito más a la izquierda tiene la posición N-1 (porque hay N dígitos), el peso de cada dígito es B^i. Dado un número con N dígitos con valores b_i (b_i\in [0\ldots B-1] y i\in [0\ldots N-1]) su valor se puede calcular como:
valor = \sum_{i=0}^{N-1} b_i\cdot 2^i = b_{N-1}2^{N-1}+b_{N-2}2^{N-2}+\ldots +b_{1}2^{1}+b_{0}2^{0}.
Por ejemplo, el número binario 10011_2 tiene el valor en decimal 1\cdot2^4+0\cdot2^3+0\cdot2^2+1\cdot2^1+1\cdot2^0=16+2+1=19_{10}. El binario nos parece extraño de entrada, mientras que el decimal no tiene misterios. Nos parecería ridículo tener que aplicar el sumatorio anterior para el número 21 expresado en decimal: 21_{10}=2\cdot10^1+1\cdot2^0=20+1=21. El motivo es que llevamos toda la vida usando esta base y los números nos parecen “normales”. Si contásemos en binario desde pequeños, el binario sería algo natural y el decimal algo artificial. No me extiendo más en este tema, pero los Mayas usaban una representación vigesimal, en la que los dígitos iban del 0 al 19, y quiero pensar que usaban estos números con total normalidad. Dicho esto, no es de extrañar que usemos base 10, puesto que solemos usar los 10 dedos de nuestras manos para contar (por eso un dígito es un dedo, pero también el guarismo que combinado forma números).

Restar sumando

Dado que en un videojuego se restan las vidas del jugador, vamos a hablar un poco de cómo restar. En concreto, cómo podemos restar números haciendo sumas. Si nos imaginamos que sólo podemos representar números decimales de 3 dígitos (que irían del 000_{10} al 999_{10}), una manera de restar una unidad sería sumar el número 999. Por ejemplo, si al número 5 (005) le sumamos 999 obtenemos el número 1004, que representado con 3 dígitos sería el 1004, es decir, el 4. Resumiendo, si sumamos el número más grande que se puede representar con los dígitos disponibles, el resultado es equivalente a restar una unidad. En binario podemos hacer exactamente lo mismo. Si utilizamos 8 bits, los números representables van del 0 al 2^8-1=255 y restar una unidad es equivalente a sumar el número 255. Si al número 5_{10}=00000101_2 le sumamos 255_{10}=11111111_2, obtenemos el número  100000100_2 que si eliminamos el noveno bit más significativo (el de más a la izquierda) nos quedaría el número 00000100_2=4_{10}. Esto que os cuento entra dentro de la computación modular, pero no puedo contar todas las matemáticas en un único post :-).

Curiosamente todo lo que acabo de contar se puede explicar mediante el uso de aritmética en complemento a 2 (C2) – no explico el complemento a la base en general, sino que me centro en base 2 para no extenderme. En la representación en C2, el bit más significativo (más a la izquierda) se utiliza como bit de signo. Los números positivos tendrían este bit a 0 y los negativos a 1. El número se obtiene de la siguiente forma: valor = -b_{N-1}\cdot 2^{N-1} + {\sum_{i=0}^{N-2} b_i\cdot 2^i} = -b_{N-1}2^{N-1}+b_{N-2}2^{N-2}+\ldots +b_{1}2^{1}+b_{0}2^{0}.

Con esto, el número 3 se representaría con 8 bits como 00000011 y el -3 como 11111101. Si hacéis las cuentas sale. Lo interesante de los números en C2 es que podemos sumarlos sin importar que sean positivos o negativos y el resultado nos dará positivo o negativo directamente, y será correcto (siempre que se pueda representar con el número de bits disponibles). Como digo, no puedo contarlo todo, pero si sumamos los números 3 y -3 en C2 se ve que el resultado es 0 (00000011+11111101 = 100000000, descartando el noveno bit). Por lo tanto, restar una unidad a un número es lo mismo que sumarle -1, que en binario con C2 es el número 11111111, y esto coincide con la idea de sumar 255.

Al lío: ¿Qué pasaba con las 255 vidas de Sinistar?

Wikipedia nos cuenta que la máquina recreativa Sinistar fue creada en 1982 por la empresa Williams Electronics. Los responsables fueron Sam Dicker, Jack Haeger, Noah Falstein (participó en varias aventuras point and click de Lucas Film Games) , RJ Mical, Python Anghelo y Richard Witt. El juego consistía en manejar una nave espacial evitando el ataque de naves enemigas, recopilando cristales de planetoides que nos permitirían ensamblar bombas, para posteriormente poder luchar contra una terrorífica fuerza cósmica con aspecto de calavera llamada Sinistar. Al aparecer Sinistar en pantalla, además de escucharse una voz terrorífica – principalmente por la baja calidad del audio (se puede escuchar en este vídeo y hay muestras de audio aquí) -, nuestra misión era utilizar las bombas adquiridas para destruir a este jefe final, con cuidado de no quedar atrapados en su campo gravitatorio. Si esto ocurriese, seríamos irremediablemente atraidos hacia su centro de gravedad y nuestra nave explotaría, perdiendo una vida.

Es en este último punto donde radicaba el truco para conseguir 255 vidas. Si nuestra nave era atrapada en el campo gravitatorio de Sinistar y, mientras se acercaba poco a poco a ésta, recibía el impacto de un proyectil enemigo, el contador de vidas se veía decrementado en 2 unidades. Si teníamos justamente una vida el número de vidas pasaba a ser 255. Es bastante divertido escuchar a uno de los programadores (Robert Mical) hablar sobre este tema.

Se puede explicar razonablemente el glitch con lo que ya sabemos:

• El hecho de que el contador de vidas pase a tener el número 255 nos está indicando que la variable asociada al mismo era una variable de 8 bits (255 es el número más grande que se puede representar con 8 bits), lo cual no es de extrañar dadas las fechas.
• Según Robert Mical, una vez que nuestra nave era capturada por Sinistar, los disparos de las naves enemigas no se tenían en cuenta. Sin embargo, los proyectiles que ya estuviesen en el espacio antes de haber sido atraidos por el campo de fuerza del jefe final sí podían destruirnos. Este aspecto no está del todo claro, de hecho, lo mejor sería reproducirlo jugando (si os animáis y os sale me contáis por favor 😉 )
• Todo apunta a que durante la captura de la nave por Sinistar se seguía llamando a la rutina que comprobaba las colisiones con los proyectiles y que si ocurría alguna se restaba una vida. Al explotar la nave volvía a restarse una vida como parte de la rutina de atracción gravitatoria y el contador  de vidas se situaba en 255 vidas.
• Si pensamos que para terminar el juego, las vidas deberían ser cero, entonces nunca acabaría éste, puesto que esta condición no se cumple.
• Si en lugar de comprobar si el contador de vidas es cero se comprueba si es menor que 1, tampoco se cumpliría. Aquí hay que destacar que el número 255 también puede interpretarse como -1 en C2 con 8 bits, pero todo esto sólo es una interpretación del programador y el programa debe utilizar las instrucciones adecuadas para considerar si el número es sin signo o con signo.  Esto es muy importante puesto que las instrucciones que ejecuta la CPU para, por ejemplo comprobar si el número de vidas es menor que uno para un número positivo o para un número con signo son diferentes.
  • Si usamos instrucciones pensadas para números positivos (sin signo) y el contador de vidas vale 255, entonces nunca se detectará que ha terminado la partida porque 255 no es menor que uno, al margen de que nosotros sepamos que este número también puede ser un -1 en C2.
  • Si se hubiesen utilizado instrucciones para números con signo se podría haber detectado que el número de vidas era negativo.  Pero ¿para qué se iban a usar estas instrucciones si el número de vidas nunca debería ser negativo? Y es aquí donde radica el problema con los glitches (también llamados bugs de programación) y es que ocurren porque no se consideran todos los casos y suelen ser difíciles de detectar.
• Por último, me he interesado en saber qué microprocesador utilizaba esta máquina recreativa. Según el manual de instrucciones que hay en https://www.arcade-museum.com hay dos micros de Motorola: 6809E y 6808. Se indica que el 6809E forma parte del sistema de vídeo y el 6808 del sistema de audio. ¿Y el programa principal dónde corre? El manual no da muchos detalles, pero hay una placa que contiene la CPU y las ROMs. Pero el esquema que proporcionan de esta placa sólo muestra las ROMs.

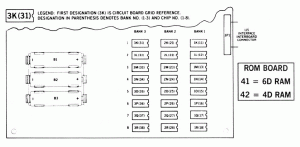
Williams Electronics (c) 1983

En eBay he encontrado fotos de las placas y he podido comprobar que la CPU es el micro 6809E.  Un poco confuso todo esto. Destacar que este micro, que combinaba operaciones de 8 y 16 bits, se usó en ordenadores como el Tandy TRS-80 Color Computer y el Dragon 32, en la consola Vectrex y en las recreativas Defender, Gyruss, etc.

Con esto termino esta nueva entrada. Al margen de la idea básica del glitch, que espero que os haya gustado, una vez más ha quedado patente lo dificil que es encontrar detalles tan sencillos como qué CPU utilizaba una máquina recreativa. El tiempo pasa y estos detalles se van perdiendo si no los preservamos.

¡Hala! A echar una partidita a Sinistar.