Nov 08 2019

Composición para chips de audio de 8 bits: Introducción informal a la música

Esta entrada pretende ser una introducción muy informal a conceptos musicales que se necesitan para comenzar en el mundillo de la música de 8 bits, o música chiptune. Las ideas son generales aunque se utilizará un programa de composición concreto (Arkos Tracker 2) orientado a un chip concreto (AY-3-8910). Creo que no es difícil extrapolar a otros programas (llamados trackers) o a otros chips.

Insisto en el punto de que la introducción será informal. Mi objetivo es contar lo mínimo para que podamos empezar lo antes posible a componer con trackers. Muchas cosas se irán desarrollando en próximas entradas.

 

Música para sistemas de 8 bits

Con esto nos referimos a componer música que va a ser interpretada por sistemas digitales de 8 bits que poseen chips de audio de los años 80. Es decir, crear canciones para programas o videojuegos de máquinas como la Nintendo Gameboy, NES y ordenadores MSX, Spectrum, Commodore, etc., o incluso a máquinas recreativas. Puede crearse cierto dilema si consideramos que internamente los chips de audio no tienen por qué ser sistemas digitales de 8 bits. Suelen tener un interfaz de 8 bits mediante el cual se le envián comandos para que se generen los sonidos, pero internamente pueden funcionar con más bits, o incluso con componentes analógicos. De todas formas, al decir que son chips de los años 80 y que se asociaban principalmente a videojuegos de los sistemas de la época, creo que se simplifica todo esto.

De forma breve comento que estos chips de audio son capaces de generar sonidos y de ahí su capacidad de generar música o efectos de sonido. Normalmente existe una limitación en el número de sonidos simultáneos que se puede generar. A cada sonido independiente le llamaré una voz o canal. Por ejemplo, se pueden usar varias voces para crear una melodía (supuestamente agradable al oído) y dedicar alguna otra voz a hacer efectos de disparo, o explosiones o choque. Las voces en los chips más primitivos se basaban en ondas cuadradas (cambios bruscos en la amplitud de la onda acústica oscilando entre dos únicos valores: amplitud baja y amplitud alta) y en ruido (cambios aleatorios en la amplitud utilizando gran cantidad de valores). En un rato doy más detalles, tranquilos. Las ondas cuadradas se utilizaban para melodías y efectos y el ruido para la percusión y para efectos sonoros (explosiones, golpes, las olas del mar…). Cuándo se producían estos sonidos y cuáles eran sus propiedades quedaba determinado por comandos que se introducían digitalmente en el chip. Realmente, lo que ocurría es que una CPU (o cualquier otro sistema digital) accedía a un puerto de entrada del chip de audio escribiendo datos en registros. Cada registro permitía modificar distintos parámetros. Por ejemplo, podíamos modificar la frecuencia y amplitud de una de las voces y posteriormente apagar su volumen. Con esto se conseguía que sonase una nota musical durante un tiempo controlado.

A continuación os pongo un ejemplo utilizando el chip AY-3-8910 (3 ondas cuadradas) en el que:

1. Suena la voz 1 (acompañamiento 1)

2. Suena la voz 2 (melodía)

3. Suena la voz 3 (acompañamiento 2) – Aquí se usan arpegios que se ejecutan muy rápido y da la

     impresión de que hay más de una nota simultánea.

4. Suenan las voces 1 y 2

5 Suenas las voces 1, 2 y 3 (se repite varias veces con una melodía más amplia)

Resumiendo:

  • Disponemos de un chip de audio
  • El chip permite generar varias voces asociadas a sonidos y ruidos
  • La generación de sonidos se produce mediante el acceso a los registros de configuración del chip

 

De acuerdo, falta mucho por explicar, pero ya dedicaré una entrada a profundizar en estos temas.

 

Notas musicales y escala

Insisto y me pongo pesado, no me importa, yo soy así: no pretendo dar un curso de lenguaje musical sino únicamente presentar lo mínimamente necesario para poder utilizar trackers. Dicho esto continúo.

Empezamos hablando de qué es el sonido. Pero solo veremos el sonido que es interpretado por el ser humano como tal. Podríamos decir que hablaremos del sonido audible y que consiste en cualquier vibración mecánica que es captada por nuestros oídos e interpretada por nuestro cerebro. El sonido necesita un medio físico para que se produzca la propagación de las vibraciones desde el origen de éstas hasta nuestros oidos. De ahí que no haya sonido en el espacio, puesto que el vacío no permite la propagación de ondas mecánicas. Os pongo un ejemplo:

Una persona (José Turing) al hablar hace vibrar sus cuerdas vocales, las cuales ponen en movimiento a las moléculas de aire de alrededor de éstas, creándose una onda. Dicha onda se propaga por el espacio debido a que las moléculas de aire chocan entre sí. Finalmente, la onda llega al oído de otra persona (María Lovelace) y transmitiéndo la vibración del aire a su tímpano. Esta vibración finalmente acaba siendo transformada en impulsos eléctricos que procesa el cerebro y que crean la percepción del sonido. El rango de frecuencias audibles por el ser humando va aproximadamente desde 20 Hz hasta 20 KHz (desde 20 variaciones por segundo hasta 20.000 variaciones por segundo).

Podríamos extender el ejemplo a qué ocurre cuando escuchamos música en con el PC (o cualquier reproductor digital). En el PC dispone del audio en un fichero, que no es otra cosa sino una colección ordenada de números. Esta secuencia de números se procesa obteniendose otra secuencia digital que se corresponden con las variaciones en el tiempo de la amplitud del sonido y que es análoga a la onda acústica. Estas variaciones se transforman en variaciones de la amplitud de una tensión eléctrica que excita mediante inducción la membrana de un altavoz (auricular) la cual vibra haciendo vibrar las moléculas de aire , comenzando así un proceso similar al descrito en el párrafo anterior. Podríamos también buscar la similitud entre el funcionamiento del oído y el de un micrófono, pero mejor paro ya con los ejemplos :).

Destacamos dos parámetros esenciales en el sonido: la frecuencia y la amplitud. La frecuencia es la velocidad de vibración y determina el tono del sonido. Variaciones lentas producen sonidos graves (teclas a la izquierda en un piano) y variaciones rápidas sonidos agudos (teclas a las derecha en un piano). La amplitud determina la intensidad o volumen del sonido.

A partir de este punto es interesante disponer de un teclado para hacer pruebas de sonido. Podéis utilizar el teclado que viene con la aplicación Arkos Tracker 2 (AT2) o cualquier teclado en línea.

PRUEBA:

  • Abrir la aplicación AT2
  • Hacer click con el ratón en las teclas más a la izquierda y escuchar su sonido [grave]
  •  Hacer click con el ratón en las teclas más a la derecha y escuchar su sonido [agudo]

Pues vamos con las escalas. Definamos nota músical  como la unidad básica con la que se componen las canciones. Una nota musical tiene un sonido diferenciado correspondiente a un conjunto de frecuencias. Las frecuencias están determinadas, no nos vale cualquiera al azar. Por ejemplo, el la de concierto tiene una frecuencia de 440 Hz (440 cambios por segundos). Si duplicamos la frecuencia obtenemos la misma nota pero una octava más alta (la nota la se encuentra a 440 Hz y a 880 Hz). Si dividimos la frecuencia entre 2 obtendríamos la misma nota pero una octava más baja (la nota la se encuentra a 440 Hz, pero también a 220 Hz). Al escuchar sonidos a frecuencias 220 Hz, 440 Hz, 880 Hz, etc., nuestro cerebro es capaz de identificar todas las nota como la, pero cada una estará en una octava diferente sonando más graves o más agudas según sus frecuencias sean bajas o altas, respectivamente.

En la siguiente muestra de audio se escuchan 6 notas.

  1. LA octava 2 de AT2 (A-2)
  2. LA octava 3 de AT2 (A-3)
  3. LA octava 4 de AT2 (A-4)
  4. DO octava 2 de AT2 (C-2)
  5. DO octava 3 de AT2 (C-3)
  6. DO octava 4 de AT2 (C-4)

 

En la figura vemos el nombre que se le da a las notas en el teclado del piano: do, re, mi, fa, sol, la, si (en notación anglosajona C, D, E, F, G, A, B). Se han representado 3 octavas completas. Las teclas de la izquierda producen notas con frecuencias bajas y conforme nos desplazamos a la derecha las frecuencias van incrementándose haciendo que las notas se hagan más agudas. Se observa la naturaleza cíclica de las notas; por ejemplo la nota do ser repite tres veces en el dibujo. Sabemos que la frecuencia de la nota do de la primera octava (la más a la izquierda) es la mitad que la frecuencia que la ntoa do que está en la siguiente octva (octava central), y así sucesivamente.

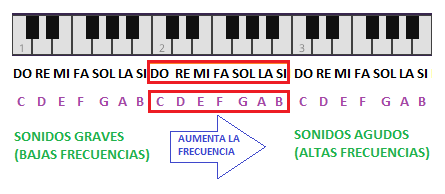
Notas musicales en el teclado del piano

PRUEBA: Intentar tocar las seis notas del audio anterior

En el sistema musical occidental utilizamos la escala cromática, compuesta por 12 notas diferentes que están separadas entre sí un semitono. La escala de doce notas es cíclica: si interpretamos las notas de forma ascendente y llegamos a la última nota – la duodécima- añadir un semitono a ésta para obtener una decimotercera nota nota implica repetir la primera nota de la escala pero en una octava inmediatamente superior. Todo esto podemos verlo en la figura anterior.

Si recorremos en orden la escala cromática se produce una sensación de ascenso (descenso si invertimos el orden), pero no realmente de melodía. Se utiliza bastante para crear ambiente de misterio, terror, tensión, etc. En la figura vemos un par de ejemplos de escalas cromáticas situadas en el teclado de un piano.

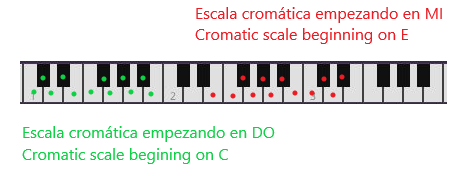
Cromatic scales beginning on C and E/Escalas cromáticas comenzando en DO y MI

Ahora escuchemos varios ejemplos:

  1. 12 notas de la escala cromática en DO
  2. “Paseo” por la escala cromática en DO
  3. 12 notas de la escala cromática en MI
  4. “Paseo” por la escala cromática en MI

PRUEBA: Practique la escala cromática.

Podemos extraer un subconjunto de notas de los 12 sonidos de la escala cromática para formar numerosas escalas nuevas cada una creando un ambiente característico: alegría, tristeza, misterio, dramatismo, etc. Nos centraremos únicamente en los denominados modos mayores y menores.

Para poder hacer esto nos falta dar nombre a las teclas negras del piano. En general si queremos expresar que una nota debe sonar un semitono más alta se indica con el símbolo # (sostenido – sharp en inglés) . Por ejemplo la nota DO# en el piano se correspondería con la tecla negra inmediatamente superior al DO (en cualquier octava). Para expresar que la nota debe sonar un semitono más baja se utiliza el símbolo ♭ (bemol – flat en inglés). Por ejemplo el SOL♭ sonaría al pulsar la tecla negra inmediatamente inferior a la tecla del SOL. Se observa que FA# y SOL♭ suenan igual. Esta redundancia está relacionada con la forma en la que se crean las escalas y para entender esto bien habría que dedicar más tiempo, pero digamos que tiene que ver con la nota base (la primera nota) de la escala que estemos usando y también con su modo (por ejemplo, mayor o menor). Veamos ahora todos los nombres de las notas (teclas):

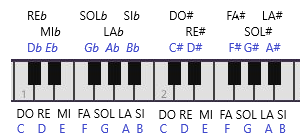
All musical notes/Todas las notas musicales

Escalas mayores y menores

Tal como he comentado, las escalas se forman eligiendo notas entre las 12 notas de la escala cromática. Deben tener una nota de referencia que se denomina nota base (o tónica) que se corresponde con la primera nota de la escala. Como hay muchas escalas, sólo nos referimos aquí a los modos mayor y menor.

Modo mayor

El modo mayor está compuesto por 7 notas y debe cumplir la siguiente relación entre las mismas:

  • 1-2: El intervalo musical entre la primera nota y la segunda es de 1 tono (2 semitonos)
  • 2-3: El intervalo musical entre la segunda nota y la segunda es de 1 tono (2 semitonos)
  • 3-4: El intervalo musical entre la tercera nota y la cuarta es de 1 semitono
  • 4-5: El intervalo musical entre la cuarta nota y la quinta es de 1 tono
  • 5-6: El intervalo musical entre la quinta nota y la sexta es de 1 tono
  • 6-7: El intervalo musical entre la sexta nota y la séptima es de 1 tono
  • 7-8: El intervalo musical entre la séptima nota y la octava es de 1 semitono

 

De forma esquemática -> Modo mayor = T-T-S-T-T-T-S

En la figura os pongo el ejemplo de DO mayor y LA♭ mayor (o SOL # mayor):

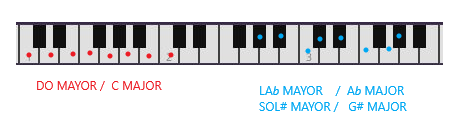
Major scales/Escala mayores

Escuchemos como suena:

  1. Do mayor
  2. La bemol mayor
  3. Do mayor una escala más alta que en 1.
  4. La bemol mayor una escala más baja que en 2.

Se observa que las notas blancas del piano se corresponden directamente con las notas de la escala de Do mayor. Además, en un piano, do mayor es la escala mayor más fácil de tocar y por eso se suelen empezar a aprender a tocar el piano con canciones en esta escala.

Se suele utilizar para expresar alegría, motivación, serenidad, etc.

PRUEBA: Interpretar en el piano las escalas de DO mayor, SOL mayor, RE mayor y Si♭ mayor.

Modo menor

De forma esquemática -> Modo menor = T-S-T-T-S-T-T

En la figura os pongo el ejemplo de LA menor y DO menor:

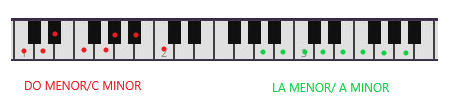
Minor scales/Escalas menores

Se observa que las notas blancas del piano se corresponden directamente con las notas de la escala de LA menor. De nuevo, la menor es la escala menor más fácil de tocar y por eso también se suele comenzar a aprender a tocar el piano con canciones en esta escala.El modo menor se utiliza para expresar tristeza, tensión, etc.

 

PRUEBA: Interpretar en el piano las escalas de LA menor, DO menor, RE menor, FA# menor.

Mayor vs menor

En este tutorial nos ceñiremos al uso de Do mayor y La menor únicamente. Ahora vamos a hacer un experimento sencillo:

  1. Componemos una canción en Do mayor y la escuchamos
  2. Luego desplazamos todas las notas dos teclas blancas (ojo que no estoy diciendo semitonos, ni tonos). Es decir las notas Do, Re, Fa las transformamos en La, Si, Re.
  3. Escuchamos ambas canciones seguidas.

 

Vamos a ello:

1. Canción en Do mayor:

Do-3 Re-3 Mi-3 Sol-3 — Do-3 Re-3 Mi-3 Sol-3  – (pausa) La-3 Si-3

Do-4 Re-4 Mi-4 Sol-4 — La-4 Mi-4 La-4 Re-4     – Do-4

2. Canción desplazado (a La menor)

La-2 Si-2 Do-3 Mi-3 — La-2 Si-2 Do-3 Mi-3 – (pausa) Fa-3 Sol-3

La-3 Si-3 Do-4 Mi-4 — Fa-4 Do-4 Fa-4 Si-3     – La-3

3. Lo escuchamos:

Creo que se ve claramente el efecto que produce cada tonalidad.

Cosas que se quedan en el tintero

El tintero es enorme porque me dejo practicamente todo: ritmo, tonalidad, etc. Estas cosas las iremos viendo de forma práctica en próximos articulos.

Por lo pronto, animo a los más valientes a que vayáis componiendo con Arkos Tracker 2. Cuatro pasos, que desarrollaré más en otro momento, pero que puede que os sirvan para ir probando cosas:

  1.  Abrir Arkos Tracker 2
  2. Nada más abrilo siempre aparece el instrumento “First”. Usad el ratón para “pulsar” las teclas del piano y escucharlo.
  3. Para poder componer hay que activar el modo edición pulsando en el icono de “REC” (ver figura [me ha quedado regular, lo sé]).
  4. En la zona de patrones (“pattern”) podéis introducir notas en la primera columna. Las voces están indicadas con los número 1, 2 y 3 en un recuadro verde. Las notas se introducen con el teclado del ordenador:

Z=DO

S=DO#

X=RE

…

Q=DO (octava superior)

2=DO # (octava superior)

…

    5. Al pulsar el icono de “PLAY” se reproducirá la canción.

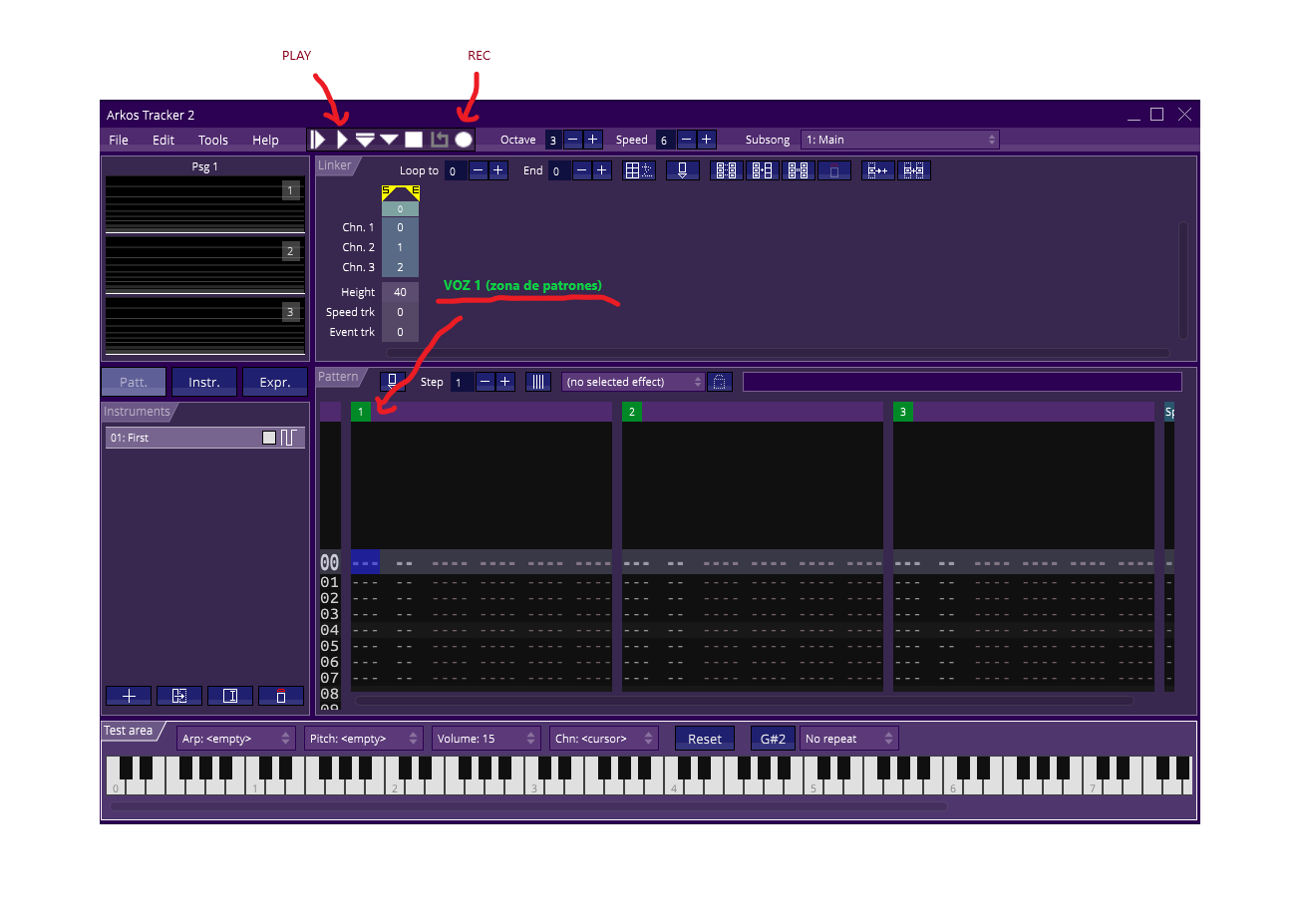
Arkos Tracker 2

 

Nuevo (10/11/2019): He preparado una “Introducción minimalista a Arkos Tracker” para que sea más sencillo arrancar con la herramienta y para poner en práctica los temas que hemos tratado en este artículo.

 

Aquí lo dejo, pronto empezaremos a aprender a usar el tracker y veremos trucos de composición para 8 bits.

¡Practicad las escalas!

 

 

Jul 29 2019

Conversión rápida de binario a decimal – Parte II

[Conversión de binario a  decimal – parte I]

(Traducción del inglés de la entrada Fast binary conversion – Part II  publicada el 30/3/2019)

En esta entrada continuaremos hablando de la conversión rápida de números binarios,  esta vez centrándonos en números con signo, y en particular, en números en complemento a dos (C2).  Los números binarios se introdujeron en un post anterior (Sinistar),  donde además se trató brevemente de los números en C2:

“En la representación en C2, el bit más significativo (más a la izquierda) se utiliza como bit de signo. Los números positivos tendrían este bit a 0 y los negativos a 1. El número se obtiene de la siguiente forma: valor = -b_{N-1}\cdot 2^{N-1} + {\sum_{i=0}^{N-2} b_i\cdot 2^i} = -b_{N-1}2^{N-1}+b_{N-2}2^{N-2}+\ldots +b_{1}2^{1}+b_{0}2^{0}.

Con esto, el número 3 se representaría con 8 bits como 00000011 y el -3 como 11111101. Si hacéis las cuentas sale. Lo interesante de los números en C2 es que podemos sumarlos sin importar que sean positivos o negativos y el resultado nos dará positivo o negativo directamente, y será correcto (siempre que se pueda representar con el número de bits disponibles). Como digo, no puedo contarlo todo, pero si sumamos los números 3 y -3 en C2 se ve que el resultado es 0 (00000011+11111101 = 100000000, descartando el noveno bit). Por lo tanto, restar una unidad a un número es lo mismo que sumarle -1, que en binario con C2 es el número 11111111… “

Pues nada, veamos si podemos encontrar maneras de leer numeros binarios en C2 de forma rápida.

Números positivos

Los números positivos son aquellos que poseen un cero en el bit más significativo (MSB, del inglés: most significant bit). Así que el peso negativo, que es el del bit más significativo, queda multiplicado por cero por lo que el valor del número es positivo. Por ejemplo, el número en C2 011 es 3, porque 011_2=(-2^2)\times 0 + 2^1\times 1 + 2^0\times 1 = 3_{10}. Por lo tanto, si el MSB es cero, los números son positivos y podemos aplicar todas las reglas que vimos en la parte I.

A partir de este punto nos centramos en números negativos.

Todos unos

Un número de N bits con N unos es siempre igual a -1_{10}. El motivo es bastante claro:

111 \cdots 111_{2}=1000 \cdots 000_2+011 \cdots 111_2=(-2^{N-1})+(2^{N-1}-1)=-1_{10}

Aquí hemos aplicado la regla de los “unos consecutivos” para el segundo término de la suma. Con esto:

1_2=-1_{10}

 

11_2=-1_{10}

 

111_2=-1_{10}

…

1111111111_2=-1_{10}

Etc.

Más unos que ceros

Un número con más unos que ceros puede verse como un número formado por unos en su totalidad con algunos unos que han sido restados. Por ejemplo:

111101_2=111111_2-000010_2=-1_{10}-2_{10}=-3_{10} 1111010111_2=1111111111_2-0000101000_2 = -1_{10}-40_{10} = -41_{10}

Es sencillo inferir del ejemplo que una forma de leer los números negativos en C2 es invertir los ceros y unos, añadir una unidad y luego aplicar el signo negativo.  De esta manera, un número negativo B puede convertirse a decimal aplicando la operación -(\bar{B}+1)=-\bar{B}-1. Por ejemplo, 111101_2=-000010_2-1 = -2-1=-3. Así que ahora puedes elegir entre “ver” los números negativos como el número -1 al que le faltan “unos” justo donde están los ceros, o como el resultado de multiplicar -1 por el número binario invertido, menos uno.

Más ceros que unos para números negativos

Si hay más ceros que unos puede ser una buena opción simplemente sumar los pesos de los dígitos que valen unos:

10000001_2= -2^7+1=-127

 

1000101_2= -2^6+4+1=-59

 

1000000000_2= -2^9=-512

 

Ceros a la derecha

Al igual que ocurría con números sin signo (y números positivos en 2C), el efecto de tener ceros a la derecha es equivalente a multiplicar por una potencia de dos. PAra números negaticos tenemos:

10100_2=101_2\cdot 2^2=-3\cdot4=-12

1111111111000_2=1111111111_2\cdot 2^3=-1\cdot 8=-8_{10}

11110101110000_2=1111010111_2\cdot 2^4 = -41_{10}\cdot 16 = -656_{10}

100010100_2=1000101_2\cdot2^2= (-2^6+4+1)\cdot 4=-61\cdot 4 = 244_{10}

Etc.

Juntémoslo todo

Ahora lo juntamos todo con el objetivo de intentar encontrar la forma más eficiente de realizar la conversión rápida de varios números en C2.

010100000101=1024+256+5=1285

10100000101=-6\cdot128+5=-768+5=-763

011110000=15\cdot16=240

11110000=-1\cdot16=-16

011110111000=(255-8)\cdot8=247\cdot8=1976

11110111000=-9\cdot8=-72

Etc.

Con esta entrada y con la anterior (parte I) creo que hemos aprendido algunos trucos que pueden ser útiles si no disponemos de una calculadora a mano. Queda abierto el tema de si con lo que hemos aprendido podremos comunicarnos con soltura con los vaporizadores de humedad. Me vais contando.

Jul 25 2019

Un telegrama sobre el datagrama: Breve historia de OSI

[Traducción de la entrada A telegram about the datagram: Short history of OSI publicado el 6/1/2019]

Breve historia de OSI

Esta entrada se basa en el artículo “The Internet that wasn’t” by Andrew L. Russell [Russell13] publicado en la revista IEEE Spectrum en 2013. El autor es profesor de Historia en el Stevens Institute of Technology, New Jersey, EE.UU. y escribió un artículo anterior sobre OSI en 2006 [Russell06] pero decidió actualizarlo en 2013. El objetivo de esta entrada es presentar (telegráficamente) un resumen de sus contenidos, así que si estás realmente interesado en el tema te recomiendo que leas los artículos originales.

El profesor Russell se animó a actualizar la información tras recibir varios emails de veteranos de OSI (Open System Interconnection standard) quejándose sobre la forma en la que Ruseel había descrito el estándard en [Russell06]. Escribió un libro contando la historia de OSI en 2014 [Russell14].

Introducción

A finales los 70 un grupo de personas destacadas de la industria de la computación de Francia, R.U. y EE.UU. comenzaron a desarrollar un standard para redes de ordenadores . Este estándard se llamó OSI: Open Systems Interconnection. Su misión era la de habilitar un intercambio de información global.  En 1980 miles de ingenieros estaban involucrados en el proyecto y OSI parecía que iba a ser una realidad. Sin embargo, en 1990, OSI estaba parado y TCP/IP fue el estándard que se adoptó para las comunicaciones a nivel mundial.

Esta historia comienzo en los años 60.

1960

En esta era las comunicaciones entre ordenadores era un tema muy activo. La conmutación de paquetes Packet switching emerge siendo Paul Baran (Rand Corporation, EE.UU.), y Donald Davies (National Physics Lab, R.U.) las personas detrás de esta técnica. La idea consiste en que los datos se descomponen en bloques discretos (paquetes) que se encaminan de forma separada y se ensamblan de nuevo en el receptor para obtener el mensaje original. Esto era más eficiente que la conmutación de circuitos que se basaba en predeterminar el camino completo entre el transmisor y el receptor.

En 1969 investigadores del DARPA (Defense’s Advanced Research Projects Agency) crearon la primera red de conmutación de paqutes: ARPANET. IBM y monopolios telefónicos de europa comenzaron proyectos similares. IBM imitaba el comportamiento de la conmutación de circuitos con los llamados circuitos virtuales, reutilizando la tecnología prestablecida. El resultado es que se entorpecía el desarrollo de la conmutación de paquetes.

1970

En 1972 se crea el International Network Working Group (INWG) con la misión de estandarizar la conmutación de paquetes. Los páises implicados eran EE.UU., R.U. y Francia. Destacan como miembros especialmente activos Vint Cerf (EE.UU., primer presidente del INWG) y  Louis Pouzin (Francia).

Pouzin – lider de Cyclades, el proyecto francés sobre conmutación de paquetes- propuso la idea del datagrama: los paquetes se envían sin crear una conexión. El INWG apoyó esta idea del datagram.

En 1974 Cerf y Robert Kahn (DARPA) publicaron las bases de Internet desarrolando las ideas de Pouzin [Cerf74].

En 1975 el protocolo de red se envió al (Consultative Committee for International Telegraphy and Telephony), but fue rechazado. INWG le echó la culpa de la negativa a  los defensores de la conmutación de circuitos. En este mismo año (1975) Cerf se marcha al DARPA y allí trabaja con Bob Kahn.

En 1977 R.U. propone al ISO (International Standardization Organization) la creación de un estándar para la conmutación de paquetes, idea que es apoyada por Francia y EE.UU. El objetivo era poder interconectar cualquier tipo de ordenador. Este estándar supondría romper con el monopolio de las grandes compañías. Y con esto comenzó la creación del “Open Systems Interconnection”: OSI.

Charles Backman (experto en bases de datos) fue el presidente del comité. Propuso un modelo basado en la arqutiecture de IBM llamada IBM Systems Network Architecture. Sin embardo, OSI defendía la heterogeneidad  y esto fue bien recibido por muchas compañías que disponían de muchos tipos de sistemas informáticos diferentes (como por ejemplo, General Motors).

Finalmente, Pouzin abandona el proyecto francés sobre conmutación de paquetes en 1978, después de luchar por conseguir financiación por parte del gobierno francés.

El modelo OSI se basad en capas que permitían que existiera modularidad, por lo tanto, se crearon muchos comités y grupos de trabajo diferentes para cada capa. Para conseguir que se convirtiera en un estándar internacional fue necesario cumplir los siguientes 4 pasos impuestos por ISO:

  1. Borrador de trabajo
  2. Propuesta de borrador de estándar internacional
  3. Borrador de estándar internacional
  4. Estándar internacional

 

La primera reunión plenaria se celebró el 28 de febrero de 1978. Asistieron 10 países y observadores de organizaciones internacionales. IBM se las apañó para convercer a OSI de que incluyera muchos de sus intereses de negocio.
OSI forjó una alianza con CCITT, de manera que … ¡volvió la guerra entre el datagrama y el circuito virtual! Se incluyeron ambos puntos de vista en la complejidad de OSI. Crónica de una muerte anunciada: numerosas capas, muchos socios involucrados, datagramas, circuitos virtuales…

1980

El modelo de referencia OSI se publicó como un estándar internacional en 1984. Incluía estándares individuales para:

  • protocolos de transporte
  • correo electrónico
  • gestión de red
  • etc.

 

Mientras tanto, EE.UU. desarrolaba TCP/IP el cual fue adoptado como el protocolo de Internet (Internet Protocol) en 1983. Curiosamente, el grupo TCP/IP se unió a OSI en 1985 con la intención de aplicar las capas de OSI al modelo TCP/IP. También querían que todos los ordenadores de EE.UU. cumpliesen con la norma OSI en el año 1990.

En 1989 OSI todavís está bajo desarrollo y la gente de OSI estaba preocupada:

  • Se había invertido una gran cantidad de dinero por parte de compañías, EE.UU. y la Comunidad Europea.
  • Internet se presentaba bastante atractivo y ya estaba funcionando (¿qué sentido tenía OSI pues?).

 

1990

A mediados de 1990 estaba claro que OSI no iba a ser una realidad.  Los problemas principales fueron:

  • Demasiados socios
  • Demasiada burocracia
  • Demasiada complejidad

 

Internet fue adoptado debido a que:

  • Los estándares de Internet eran grátis, mientras que los de OSI no lo eran
  • Ya estaba en marcha (en EE.UU.)
  • Promovía la distribución de información de forma abierta

 

OSI fue visto como un estándar incomprensible, pero sí que tenía algunos puntos positivos:

  • Tenía una arquitectura mejor
  • Era más completo

 

Prueba de ello es que en 1992 la capa de rutado de TCP/IP se modificó de según las ideas de OSI. Hoy en día se sigue enseñando OSI en las universidades junto con TCP/IP.

La diferencia en la complidad entre OSI y TCP/IP se aprecia claramente en la figura siguiente:

Comentarios finales

OSI era algo interesante, pero se transformó en un monstruo difícil de domar. Finalmente, el punto de vista práctico y bien pensado de TCP/IP permitió hacer de Internet una realidad. Resumiendo: “OSI fue un suerño precisio, TCP/IP es vivir ese sueño” [Russell13].

Me gustaría terminar esta entrada dedicando un pensamiento a la Communtación de Paquetes francesa ideada por Pouzin a principios de los 70. En un universo paralelo Internet nació en Francia 😉 .

Bibliografía

[Russell13] “The Internet that wasn’t”, Andrew L. Russell, IEEE Spectrum, 2013

[Russell06] “Open Systems Interconnections (OSI) and the Internet”, Andrew L. Russell, IEEE Annals of the History of Computing, 2006

[Russell14] “Open Standards and the Digital Age: History, Ideology and Networks”, Andrew L. Russell,, Cambridge University Press, 2014

[Cerf74] “A Protocol for Packet Network Intercommunication”, V. Cerf, R. Kahn, IEEE Transactions on Communications, 1974

Jun 23 2019

Intel y las FPGAs: ¿Usarán FPGAs las nuevas generaciones de microprocesadores?

[Actualización del 2/7/2019] En esta entrada comentaré algunos detalles del impacto de la entrada de Intel en el mercado de los circuitos reconfigurable (FPGA), centrándome en los nuevos chips híbridos que combinan microprocesadores con tejido reconfigurable FPGA. El texto es complementario al siguiente programa de radio del Canal UNED, serie Informática en Radio 3, publicado el 28/6/2019:

 

¿Qué es una FPGA?

Una FPGA es un circuito integrado formado por una gran cantidad de memorias muy pequeñas, que almacenan escasos bits, y que pueden interconectarse entre sí . Cada memoria implementa una función lógica, con lo que es posible configurar la FPGA para que implemente cualquier circuito digital. Esta configuración se puede realizar tantas veces como se quiera, de igual manera que podemos cargar un programa diferente en un ordenador.

Esta capacidad de reconfiguración, hace que una vez fabricado el chip, su arquitectura interna pueda modificarse programando las memorias y las interconexiones. Esto no puede hacerse con otros chips, como por ejemplo el microprocesador, que una vez que están fabricados no es posible modificar en absoluto el funcionamiento de sus bloques internos.

Pero que esto no nos lleve a confusión, una CPU puede variar su funcionalidad modificando los valores de la memoria que contiene el programa que ejecuta el micro, pero si el micro está mal diseñado, entonces funcionará mal. Si el circuito digital que está implementado en una FPGA está mal diseñado, siempre puede corregirse y actualizarse, aunque ya esté el dispositivo en el mercado.

Esto es similar a las actualizaciones de Windows, que permiten corregir errores en el software de este sistema operativo, sólo que en la FPGAs las actualizaciones modifican el hardware.

El nombre FPGA viene del inglés, Field-Programmable Gate Array. En español podría traducirse como matriz de puertas programable in situ, haciendo hincapié en que puede modificarse una vez está el chip en uso. Personalmente, creo que el nombre es poco acertado, porque en realidad está compuesto principalmente de memorias y no de puertas lógicas. Un nombre más acertado hubiese sido FPLCA: Field-Programable Logic Cell Array. De hecho, la primera FPGA se llamó LCA: Logic Cell Array [Trimberger2015].

 

¿Por qué no se usan siempre las FPGAs para evitar vender productos con errores?

Tal como he comentado antes, las FPGAs puede actualizarse. Recordemos el caso del Intel Pentium que salió al mercado con un error en la operación de la división y que supuso grandes pérdidas a Intel [Cipra1995]. Más actuales son los problemas de seguridad producidos por las vulnerabilidades tipo Spectre [Abu-Ghazaleh2019], que se deben, fundamentalmente, al diseño de la propia arquitectura hardware de procesadores de Intel, ARM y AMD. Sería ideal poder actualizar nuestros procesadores a nivel hardware en lugar de tener que aplicar parches al sistema operativo, que mejoran la seguridad pero ralentizan el tiempo de ejecución de las aplicaciones.

Una FPGA puede implementar cualquier tipo de circuito digital incluyendo al microprocesador. Entonces ¿por qué no están todos los micros basados en FPGA y así poder corregir errores hardware en la etapa post-venta? El motivo es que la FPGA no es tan eficiente como un circuito específico, tal como el microprocesador.

Hay que entender que en la FPGA la mayoría del silicio área del chip está dedicada a las interconexiones. Hacer que un circuito disponga en su interior de cientos de miles de bloques que pueden interconectarse entre sí de forma arbitraria hace que el circuito aproveche muy mal el espacio. La flexibilidad va reñida con la eficiencia. Podemos imaginar las interconexiones como una red de carreteras con varios niveles, como si se tratase de los llamados “scalextric” que encontramos en algunas ciudades. Por lo tanto la FPGA no es capaz de alcanzar la velocidad de procesamiento  de los microprocesadores de Intel, ARM o AMD.

 

¿Cuál es el nicho de la FPGA?

La FPGA es interesante cuando se quieren realizar muchas tareas al mismo tiempo. Un microprocesador ejecuta las instrucciones de un programa de forma secuencial, es decir, una instrucción tras otra. Sin entrar en detalles de arquitectura de computadores, la tendencia es añadir varias CPUs en un mismo micro para así poder ejecutar varias programas (o hilos) a la vez. Los microprocesadores que usamos en casa suelen tener entre 4 y 8 CPUS (los llamados cores).

Una FPGA dispone de cientos de miles de elementos muy simples que pueden trabajar en paralelo. Si las tareas a realizar son sencillas, entonces se pueden conseguir velocidades de procesamiento abismales. Hay trabajos en la literatura académica que muestran como algunos algoritmos/aplicaciones corren hasta 10.000 veces más rápido en una FPGA que en un core de un procesador Intel i7 [Pérez2016].

Por otra parte, no solo es que estas tareas se realizan rápido, sino que al estar los diseños optimizados para algoritmos concretos, el consumo de potencia es menor que en un microprocesador, puesto que no hay hardware sobredimensionado.

Y podríamos volver a preguntarnos por qué no implementamos todos los algoritmos en FPGA y no usamos los micros. La respuesta es que no todos lo algoritmos o aplicaciones son adecuados para la arquitectura hardware de una FPGA. Y por otra parte, el diseño de estos circuitos es muy costoso en tiempo. Lo que en software se puede desarrollar en varios minutos, podría tardarse varios días en hacerlo para que se aprovechen las características de las FPGAs. Además, los tiempos de compilación de software son muy cortos en comparación con los tiempos de compilación de las FPGA.

Mundos muy distintos, pero complementarios.

Por último, comentar que un circuito optimizado para llevar a cabo una aplicación específica no sólo puede implementarse en una FPGA, sino que puede implementarse en un circuito integrado que no sea flexible y que una vez fabricado no permita variar sus interconexiones (ASIC: circuito integrado de aplicación específica). Con esto se conseguiría la máxima velocidad y el mínimo consumo de batería, pero, una vez más, si hay un error en el diseño, se perdería mucho dinero

Un poco de historia

En esta sección me baso principalmente en la información contenida en [Trimberger2015].

La primera FPGA la fabricó la compañía estadounidense Xilinx en 1985. Era el chip XC2064, al que bautizaron como LCA (logic cell array). En 1988, otra compañía del sector, Actel (ahora Microsemi), introdujo el nombre FPGA, que es como se conoce hoy en día a estos dispositivos. Estas FPGAs primitivas no eran muy útiles. Presentaban una idea interesante, pero eran caras y tenían poca capacidad.

El chip XC2018 fue el hermano mayor de la FPGA XC2064. Fuente: https://commons.wikimedia.org/wiki/File:Xilinx_XC2018_LCA.jpg

Un año antes, la compañía Altera introduce en el mercado un chip llamado CPLD (complex programmable logic device). Este chip sí que era funcional y supuso un hito en los circuitos integrados. La CPLD se basaba en una idea similar a la de la FPGA, pero utilizando puertas lógicas.

A mediados de los 90, es esta misma compañía, Altera, la que realiza un cambio drástico en las FPGAs. Las primeras FPGAs sólo permitían que se interconectasen bloques cercanos entre sí, por lo que para conectar dos bloques separados había que dividir las interconexiones en varios tramos. Algo similar a utilizar el metro, que para ir de una estación a otra, hay que pasar por todas las estaciones intermedias. El nuevo cambio fue posible a que la fabricación de chips mejoró en lo referente a interconexiones, permitiendo que existiesen varias capas paralelas por las que podían trazarse líneas conductoras (la idea del “scalextric” mencionado antes). Altera combinó líneas conductoras cortas para las comunicaciones cercanas y líneas largas para conectar bloques alejados. Con esto la FPGA empezó a ser un dispositivo mucho más flexible y rápido que la CPLD.

Con el comienzo del milenio los avances en la microelectrónica permitieron que las FPGAs tuviesen una capacidad cercana al millón de puertas lógicas y además permitió introducir elementos de procesamiento más complejos que las pequeñas memorias utilizadas hasta entonces. Se añadieron bloques de memoria RAM de varios kilobits, operadores matemáticos como multiplicadores y sumadores, e incluso microprocesadores (PowerPC de Motorola).

Esta tendencia continúa hoy en día, pero en lugar de introducir varios microprocesadores en la FPGA, éstos están fuera – aunque comparten el mismo encapsulado y se conectan directamente a gran velocidad – y son mucho más potentes. Por ejemplo, hay chips en los que conviven procesadores ARM de la familia A con dos cores, frecuencia de reloj de 1 GHz, 1 GB de RAM y una FPGA.

Me estoy centrado únicamente en las compañías más potentes de FPGA que son Xilinx y Altera, pero existen varias compañías muy interesantes en el mercado y cada una da una solución diferente: bajo consumo, seguridad, altas prestaciones, etc. Podríamos decir que tradicionalmente Xilinx y Altera ha sido las empresas líderes del sector; competidores acérrimos y que se han ido turnando a la hora de introducir innovaciones tecnológicas.

En 2015 la compañía Intel adquiere la empresa Altera por 16,700 millones de dólares, haciendo temblar los cimientos del negocio de los circuitos reconfigurables.

 

Intel entra en juego

La compra de Intel se debe principalmente a un intento por parte de esta compañía de buscar una tecnología rompedora que le permita sostener su negocio frente a la actividad de empresas como NVvidia (productor principal de tarjetas gráficas) y ARM (productor principal de microprocesadores y microcontroladores de bajo coste y bajo consumo). Nvidia domina el mercado de las tarjetas gráficas (GPU) y ARM domina el mercado de los smartphones, las tablets y los dispositivos IoT.

Tal como he comentado antes, la unión de microprocesadores y FPGA ya existía, pero nunca se había producido desde una misma empresa, y al gigante de los microprocesadores, con más de 40 años de vida, hay mirarlo siempre con mucho respeto.

En los dispositivos existentes en el mercado que combinan desde principios de la década procesadores ARM y FPGAs (por ejemplo, los chips Zynq de Xilinx o los Stratix V GX de Altera) el microprocesador se comunica con la FPGA para configurarla y para enviarle datos o recibirlos, pero pueden perfectamente funcionar de forma autónoma sin la FPGA. LA FPGA actuaría como co-procesador, es decir, como acelerador de algoritmos. El proceso de diseño de los aceleradores es lento, y aunque se han incluido compiladores que permiten usar lenguajes como C o OpenCL, se tarda entre minutos u horas en obtener un circuito disponible. Esto descarta la compilación a demanda, según se ejecuten los programas. Con esto, lo que ocurre es que hay que disponer de una biblioteca de diseños precompilados, que el microprocesador utilizará según la aplicación que esté ejecutando.

La aportación de Intel en este sentido es introducir las FPGAs en microprocesadores de altas prestaciones, como los Xeon. En 2015, Intel anuncia que integrará FPGAs en sus microprocesadores y con el objetivo de mejorar la eficiencia de aplicaciones específicas, tales como servicios en la nube, Big Data, análisis genómico, compresión de ficheros, etc. El salto a sistemas de altas prestaciones diferencia estos chips de los que hay actualmente disponibles, más orientado a aplicaciones de prestaciones bajas o medias. En este año hace un llamamiento a la comunidad científica para explotar las posibilidades de un nuevo chip que integre FPGA y microprocesadores. Es el proyecto HARP: Hardware Acceleration Research Program.

En mayo de 2018, Intel anuncia que ya tiene un prototipo que integra un chip Xeon, posiblemente un Xeon SP-6138 con 20 cores, con una FPGA Arria 10 integrada [Priaocket2018]. Existe un canal de comunicación de alta velocidad entre la FPGA y la CPU y además, como ocurre con este tipo de procesadores, es posible conectar con uno de estos canales otro procesador Xeon, que a su vez también puede disponer de una FPGA integrada. La FPGA seleccionada dispone de una capacidad de unos 10 millones de puertas lógicas, la posibilidad de hacer 3000 multiplicación de enteros simultáneas, 400 operaciones de coma flotante de precisión doble simultáneas, 2000 memorias de 2 KB, etc.

Las noticias son que han conseguido aumentar el rendimiento de técnicas de virtualización en la nube, reduciendo la latencia por dos, aumento el flujo de datos por 3 y duplicando el número de máquinas que pueden desplegarse [Pricket2018].

La respuesta del otro grande de la electrónica, Xilinx, ha sido presentar chip orientados a la aceleración que integran, además de tejido configurable FPGA, varios procesadores ARM de las familias A y R, procesadores vectoriales para Deep Learning y memorias de alta capacidad de almacenamiento y bajas latencias de acceso.

 

Límites y futuro de la tecnología híbrida

La información de la que dispongo acerca de las posibilidades de esta tecnología híbrida es bastante limitada, pero a día de hoy es posible programar la FPGA con distintos aceleradores simultáneos. Esto permite acelerar más de una aplicación. Es decir, parte de la aplicación se ejecuta mediante software en la CPU y en paralelo se hacen tareas intensivas mediante el hardware de la FPGA. Es posible crear una librería de aceleradores (denominados cores) y ejecutarlos a demanda. Los cores se varían desde la CPU como hilos que se ejecutan en paralela y es posible la comunicación entre estos hilos mediante memoria compartida.

El diseño de los cores se realiza mediante herramientas de Intel. No es un proceso sencillo, puesto que el diseño hardware no es sencillo de por sí. Con esto lo que quiero decir es que los tiempos de compilación son largos y la depuración es también costosa en tiempo. Todo esto es lo normal en el mundo del diseño de hardware digital.

Existe la posibilidad de usar lenguajes similares a C, como sería OpenCL, lo cual facilita el diseño, pero los tiempos de desarrollo siguen siendo largos. De hecho, es posible realizar compilación al vuelo, lo que permite que se use OpenCL para decribir una aplicación que correría tanto en la CPU como el la FPGA, pero seguimos teniendo el problema de que la compilación para la FPGA tarda mucho y todavía no es una opción atractiva y se está muy lejos de conseguir el tipo de compilación al vuelo que por ejemplo tenemos en GPUs y que permite que el código binario final aproveche al máximos las características de la GPU concreta que tiene conectada el ordenador.

Las posibilidades futuras son muy interesantes si entendemos que es posible hacer diseños óptimos ajustados a aplicaciones específicas con resultados realmente diferenciadores. Sin embargo, todavía, después de más de 30 años de FPGAs en el mercado, sigue habiendo grandes retos por resolver:

  • Simplificar el proceso de diseño de cores utilizando descripciones más cercanas al software que al hardware, lo que se denomina Síntesis de Alto Nivel (HLS: high-level synthesis). En mi opinión, todavía los resultados de este enfoque distan bastante de lo que se consigue con un diseño clásico en el que el diseñador toma gran parte de las decisiones. Conseguir altas prestaciones requiere entrar en un bucle de prueba y error que al final resultado también largo, aunque menos que el diseño tradicional.
  • Mejorar la conectividad con memorias de las FPGAs y con CPUs. En este sentido, estoy convencido de que Intel mejorará el sistema de cachés de las FPGAs y el acceso a memorias externas. De igual manera, hasta la fecha se han incluido líneas de alta velocidad, más orientadas a sistemas de comunicación, pero nada específico para CPUs. La FPGA debe incluir bloques similares a los que incluyen los procesadores Xeon para gestionar memorias y las comunicaciones con CPUs (enlaces QPI y UPI).
  • Reducir los tiempos de reconfiguración y mejorar las técnicas de reconfiguración parcial. En la actualidad el tiempo que se tarda en configurar una FPGA Arria 10 GX 1150 completa son de decenas de milisegundos. Además, también interesa configurar solamente parte de la FPGA por si una aplicación ha terminado y una nueva debe ejecutarse sin interrumpir la ejecución del resto de aplicaciones que siguen activas. Al igual que ocurre con el uso de memoria en ordenadores, es necesario gestionar qué zonas de la FPGA están libres y comprobar si el nuevo core encajaría en estas zonas. Lo habitual es tener un rectángulo designado a reconfiguración dinámica y usarlos siempre para esos. En definitiva, habría que dar soporte software a mejorar el rendimiento de la reconfiguración dinámica, e idealmente, modificar el hardware de la FPGA para que gestione de forma automática la introducción y reemplazo de cores a demanda.

Creo que nos encontramos en un punto de inflexión en la historia de la informática, similar al momento en el que se creó la primera FPGA, la cual presentaba una idea revolucionaria, pero las limitaciones de la tecnología y también de su propio diseño no permitieron que se desarrollase plenamente hasta pasadas un par de décadas. La introducción de computación reconfigurable en microprocesadores es una apuesta de futuro, pero todavía queda mucho trabajo por hacer. Confiemos en la experiencia de Intel para llevar esta tarea a cabo.

Agradecimientos

Tengo que agradecer a varios profesores del Departamento de Arquitectura de Computadores de la Universidad de Málaga, algunos pertenecientes al proyecto HARP, por sus comentarios: Javier Hormigo Aguilar, Rafael Asenjo y Andrés Rodríguez. Los comentarios que hago en este post son personales y no expresan su opinión.

Enlaces de interés

HARP project: https://software.intel.com/en-us/hardware-accelerator-research-program

“IEEE Chip Hall of Fame: XC2064”: https://spectrum.ieee.org/tech-history/silicon-revolution/chip-hall-of-fame-xilinx-xc2064-fpga

“FPGA for Dummies”: https://plan.seek.intel.com/PSG_WW_NC_LPCD_FR_2018_FPGAforDummiesbook

Intel FPGAs: https://www.intel.com/content/www/us/en/products/programmable/fpga.html

Xilinx: https://www.xilinx.com/products/silicon-devices/fpga.html

Lattice: https://www.latticesemi.com/Products#_D5A173024E414501B36997F26E842A31

Microsemi: https://www.microsemi.com/product-directory/fpga-soc/1638-fpgas

Referencias

[Abu-Ghazaleh2019] “How the Spectre and Meltdown Hacks Really Worked
”, Nael Abu-Ghazaleh, Dmitry Ponomarev, Dmitry Evtyushkin, IEEE Spectrum Magazine, 2019

[Cipra1995] “How Number Theory Got the Best of the Pentium Chip “, Barry Cipra, Science, 1995 [pdf]

[HARP] Website of Hardware Accelerator Research Program [link – last access 4/7/2019]

[Pricket2018] “A peek inside that Intel Xeob FPGA chip”, Timothy Pricket Morgan, The next platform, 2018 [link (last visit 2/7/2019)]

[Pérez2016] “Hardware Accelerator to Compute the Minimum Embedding Dimension of ECG Records”,  P. Pérez Tirador et al, Proceedings of International Work-Conference on Bioinformatics and Biomedical Engineering, 2016.

[Trimberger2015] “Three Ages of FPGAs: A Retrospective on the First Thirty Years of FPGA Technology”, Proceedings of the IEEE, 2015

 

Mar 10 2019

Conversion rápida de binario a decimal – Parte I

[Traducción de un artículo publicado en inglés el 24 de febrero de 2019]

El código binario es la base de los sistemas digitales y considero que es importante ser capaz de realizar la conversion a decimal de un número binario de hasta 16 bits de forma fluida. Esta habilidad te será de gran utilidad si trabajas con sistemas embebidos o en el diseño digital.

En un artículo anterior, se introdujeron las bases del sistema binario. Reutilizo uno de los párrafos::

” El binario es un sistema de representación numérica posicional en base 2. Un sistema posicional en base B representa números utilizando dígitos que pueden tomar valores entre el 0 y  B-1 (del 0 al 1 en el caso del binario; del 0 al 9 en el caso del decimal, etc.), y que se escriben uno detrás de otro. La posición i que ocupa cada dígito determina su peso. Si asumimos que el dígito más a la derecha tiene la posición 0 y que el dígito más a la izquierda tiene la posición N-1 (porque hay N dígitos), el peso de cada dígito es B^i. Dado un número con N dígitos con valores b_i (b_i\in [0\ldots B-1] y i\in [0\ldots N-1]) su valor se puede calcular como:
valor = \sum_{i=0}^{N-1} b_i\cdot 2^i = b_{N-1}2^{N-1}+b_{N-2}2^{N-2}+\ldots +b_{1}2^{1}+b_{0}2^{0}.
Por ejemplo, el número binario 10011_2 tiene el valor en decimal 1\cdot2^4+0\cdot2^3+0\cdot2^2+1\cdot2^1+1\cdot2^0=16+2+1=19_{10}. “

Aprender de memoria el valor de unas cuantas potencias de dos puede resultar útil de varias formas. En primer lugar, nos vienen bien para convertir mentalmente cualquier número binario a decimal.  Así que aplicaos y aprended las potencias de dos desde 2^0 hasta 2^{16}; es decir:  1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768 y 65536. Una vez que sepáis estas potencias de dos, es fácil determinar el mínimo número de bits que se requiere para representar en binary un número entero.  Por ejemplo, si sabemos la mayor potencia de dos más cercana al número decimal x, podremos saber el número de bits que necesita su representación binaria. Digamos que queremos converir el número 240 a binario. La mayor potencia de dos más cercana es 256=2^8, lo que nos indica que el número requiere 8 bits. Ojo, que si el número es exactamente una potencia de 2, hay que sumar una unidad al exponente de la potencia para saber el número de bits. Y por supuesto, es esencial para poder hacer la conversión rápida de binario a decimal.

Así que vayamos con los “atajos”.

Unos consecutivos

Hablemos ahora de algo bastante trivial. Si sumamos 1 al número 999, se obtiene 1000.Por lo que 999=1000-1, es decir,  999=10^3-1, y vemos que el exponente de la potencia de la base es igual al número de nueves consecutivos. Podemos generalizar para números en base B compuestos de una secuencia de N dígitos consecutivos iguales a (B^N-1)_B, y  particularizando para binario, con base (B=2), una secuencia de N unos consecutivos es igual a (2^N-1)_{10}. Así que ahora, asumiendo que dominamos las potencias de dos, podemos calcular fácilmente el valor decimal de números tales como:

    • 1111111111_2=2^{10}-1=1024-1=1023
      Etc.

Ceros a la derecha

Añadir un cero a la derecha de un número es equivalente a multiplicarlo por su base. Por ejemplo, 560_{10}=56\times10,  110_2=11_2\times 2, etc. Por lo tanto, añadir  N ceros a la derecha de un número binario es equivalente a multiplicarlo por 2^N . Esta propiedad puede ser útil en determinadas ocasiones:

10100_2=101_2\cdot 2^2=5\cdot4=20 (also, 16+4=20)

1111111111000_2=1111111111_2\cdot 2^3=(2^{10}-1)\cdot 8=1023\cdot8=8184

Etc.

Más unos que ceros

Si un número binario tiene tan solo unos cuantos ceros puede ser interesante ver el número como una serie de unos consecutivos a la que le faltan algunos unos. De esta manera, el número 111111110111_2 puede verse como 111111111111_2-1000_2=(2^{12}-1)-2^3=4095_{10}-8_{10}=4087_{10}. Veamos algunos ejemplos:

10111101_2=(2^8-1)-2^7-2^1=255-66=189

111111111100_2=(2^{12}-1)-3=4092 (ó 1023\cdot4=4092)

Vamos a juntarlo todo

Busquemos la mejor manera de realizar la conversion rápida de varios números. Asumo que se dominan las potencias de dos y que es fácil reconocer directamente números binarios pequeños.

10100000101=1024+256+5=1285

10100000101=5\cdot 2^8 + 5=5\cdot 257 = 1285

11110000=15\cdot16=240

11110111000=(255-8)\cdot8=247\cdot8=1976

11110111000=2047-64-7=2040-71=1976

1000000000001=4096+1=4097

1000000001110=4096+(7\cdot2)=4096+14=4110

111101000=8\cdot(63-2)=8\cdot61=488

Etc.

 

Ya está. No es física cuántica, pero con toda seguridad que es útil. En  numerosas ocasiones   estos trucos no serán efectivos, por lo que finalmente habrá que sumar las potencias de dos una a una para obtener el valor decimal. También se puede usar una calculadora en estos casos  🙂 .

En este artículo hemos tratado solamente números sin signo. El próximo tratará sobre la conversión rápida de números binarios con signo: números en complemento a dos.  Aplicaos bien y pronto dominaréis el lenguaje binario de los vaporizadores de humedad (¡viva Star Wars!). ¡Nos vemos pronto!

 

 

 

 

Ene 27 2019

Hello World. Hello FPGA – Parte II: Placas y fases de diseño

Continuamos con el tutorial sobre FPGAs (ver parte I). En esta entrada vamos a dar los primeros pasos para implementar un circuito (extremadamente) sencillo en una placa basada en FPGA. Creo que con esto se entenderá que el desarrollo con FPGAs difiere notablemente del desarrollo software.

Diseño con FPGA

Ya vimos que la FPGA está formada por una miríada de pequeñas memorias que se pueden interconectar. El diseño a mano es inviable, por lo que es necesario utilizar herramientas software que nos ayuden a desarrollar los circuitos.  El diseñador (que no programador) se encarga de definir los bloques que forman el sistema. Para ello, debe definir las funciones lógicas que el sistema requiere y su interconexión. No hay que confundir las funciones lógicas con las LUTs, ni la interconexión entre funciones con la interconexión entre LUTs. Son precisamente las herramientas de desarrollo con FPGAs las que se encargan de particionar las funciones lógicas en LUTs y hacer que el cableado entre LUTs sea coherente con las interconexiones originales entre funciones. Y por supuesto, las herramientas optimizan el sistema conforme lo va implementando en la FPGA, tal como haría un compilador con código que tiene que transformar en ensamblador para una arquitectura de CPU determinada.

Es momento de introducir la placa como parte del flujo de desarrollo o de diseño. La placa alberga a la FPGA además de a otros chips y componentes circuitales. La placa podemos diseñarla nosotros mismos, o comprarla ya diseñada y fabricada. Para empezar en este mundillo esta es la mejor opción, aunque tengo que decir que hacer un diseño propio permite dotar a la placa de los elementos que realmente nos interesan y así abaratar su coste, reducir su tamaño, etc.

Hay placas comerciales bastante majas orientadas a distintos ámbitos.

Nos vamos a centrar en la placa DE2-115 de Terasic  DE2-115, que se basa en una FPGA Cyclone IV de la empresa Altera (Intel FPGA). La figura muestra la placa:

 

Figura. Placa DE2-115 de Terasic (imagen extraida de la web de Terasis [enlace])

[solicitado concendido permiso para su uso]

En la placa se observa claramente la FPGA (justo encima del texto Cyclone IV) y se ve que muchos otros elementos: pantalla LCD, displays de 7 segmentos (me encantan), chips variados, botones, conmutadores, conexión GPIO (General-Purpose Input/Output). Algunos de los chips que acompañan a la FPGA en este caso son: memoria SRAM, memoria DRAM, memoria EPROM, CODEC de vídeo, CODEC de audio, controladores de USB, controladores de UART, generador de salida VGA, etc. Otras placas tendrán diferentes chips, los cuales determinan sus prestaciones. Por ejemplo, pueden tener salida HDMI, puertos micro-USB, buses de expansión de memoria, etc.

La placa dispone de un puerto JTAG (Joint Test Action Group) que permite acceder directamente a la FPGA para configurarla (o programarla) o acceder a una memoria EPROM que es la que utiliza la FPGA para auto-configurase tras el arranque. En general no es posible acceder directamente a los chips que acompañan al dispositivo reconfigurable. Sin embargo, éstos están conectados a la FPGA, por lo que su configuración la debe hacer este dispositivo.

El ejemplo que abordamos consiste en utilizar dos pulsadores, o botones, de la placa para encender un LED (Light Emitting Diode). Puesto que hablamos en la parte I de una simple puerta AND, vamos a hacer que el LED se encienda únicamente cuando se pulsen simultáneamente los dos pulsadores.

Los pulsadores están conectados mediante conductores a pines o patillas concretos de la FPGA, por lo que es posible “leer” su valor lógico (si está pulsado o no) y utilizar dicho valor como parte del circuito que implementemos en la FPGA. De igual manera los LEDs están conectados a pines concretos del chip. Estas conexiones son fijas, puesto que los conductores son pistas metálicas de la placa PCB (Printed Circuit Board) (si nos fijamos de nuevo en el texto “Cyclone IV” podremos ver unas líneas de color azul más claro que el resto de la placa, estas líneas son pistas metálicas; hay más pistas en la otra cara de la placa, e incluso en su interior). Estos pines son los pines de entrada/salida de la FPGA, los cuales pueden conectarse a las LUTs igual que cualquier señal interna.

Por una parte, tenemos que ser capaces de indicar a las herramientas, que vamos a utilizar en nuestro circuito señales que provienen del exterior, y esto lo hacemos indicando a la herramienta que la señal a (por ponerle un nombre cualquiera) está conectada al pin número X. ¿Y cómo sabemos esto? Leyendo el manual de la placa. Si leemos el manual de la FPGA (llamada datasheet en inglés) podremos saber cuántos pines tiene el chip y sus características (niveles lógicos, si son de entrada o salida, si son entradas de reloj, la corriente que pueden proporcionar, etc.), pero, aunque todo esto es muy importante, no basta. En el manual de la placa vamos a encontrar la información acerca del uso que se le da a cada pin, es decir, qué elementos de la placa están conectados a éstos.

En el manual de la placa DE2-115 encontramos tablas donde se indica los pines que se están usando. Por ejemplo, para los cuatro pulsadores que aparecen en la esquina inferior derecha de la Figura la tabla es la siguiente:

Figura: Tabla 4-2 del manual, donde se indican los pines a los que están conectados los botones

[solicitado concendido permiso para su uso]

Hay tablas similares para los LEDs y para el resto de elementos de la placa.

Concretemos un poco más. Vamos a realizar una operación AND con el valor de dos botones y el resultado lo vamos a conectar a un LED. Las señales de entrada de la AND se llamarán KEY0 y KEY1 y la señal de salida de la AND se llamará LED0. Bien, ahora hay que decidir que botones usaremos. Por ejemplo, KEY0 se conectará al pin del botón KEY[0] (M23) y KEY1 al pin del botón KEY[1] (M21). LED0 se conectará al pin que está conectado a uno de los ocho LEDs de color verde de la placa, por ejemplo, a LED0.

Esto parece de Perogrullo, lo admito, pero tiene su importancia, y equivocarnos o confundirnos a la hora de elegir los pines puede darnos quebraderos de cabeza.

Bien, sigamos. Ya está, lo conectamos todo y hacemos una operación AND. Pues no, todavía nos falta un pequeño paso. Se tiende a asumir que el 0 lógico se corresponde con los conceptos de FALSO y OFF, y que el 1 se corresponde con VERDADERO y ON. Pero esto es totalmente arbitrario. Para saber si un botón devuelve al pulsarlo un 0 (un voltaje bajo) o un 1 (voltaje bajo) hay que saber cómo es su circuito. Para no andarme por las ramas, vemos en el manual de la placa que los pulsadores proporcionar un 1 si no se pulsa, el cual es su estado natural, y un 0 si se pulsan. Podéis ver el circuito para entender esta situación.

FIGURA. Esquemática de la conexión de los botones  (figura 4-6 del manual)

[solicitado concendido permiso para su uso]

Igual ocurre con el LED. Para saber si se enciende con un 1 o con un 0 hay que consultar el manual de la placa. En este caso se enciende con un 1 lógico (consultar el manual).

 

Dicho esto, en la misma placa hay LEDs, como por ejemplo los de los display de 7 segmentos, que se encienden con ceros. Y en otras placas lo pulsadores pueden perfectamente generar un 1 al pulsarse. Moraleja: hay que consultar el manual de la placa.

 

Gráficamente vemos lo que tenemos que implementar:

Figura. Esquema del diseño del ejemplo.

¿Cómo conseguirlo? Hablemos de las herramientas.

 

Fases de diseño con FPGAs

  1. Entrada de diseño

En esta fase se describe el circuito. El circuito puede describirse gráficamente utilizando puertas lógicas o bloques elementales, como multiplexores, decodificadores, contadores, etc., pero si el circuito es complejo se suelen utilizar lenguajes de descripción hardware o HDLs (del inglés, Hardware Description Languages). No confundir con lenguajes de programación: la FPGA se configura, no se programa. De forma muy simple os digo que mientras que en un lenguaje de programación el orden o secuencia de las instrucción influye en su comportamiento, todo lo que se escribe en HDL genera funciones lógicas y además todas las funciones existen y se “ejecutan” a la vez, por lo que el orden de las instrucciones que usemos en HDL no es relevante (esto es una simplificación muy grande, pero nos vale de momento). Destaco como HDLs los lenguajes VHDL y Verilog. En la actualidad hay formas de diseñar con FPGAs más cercanas a los lenguajes de programación, pero voy a evitar hablar de ellas en este momento.

  1. Simulación funcional

Una vez descrito el circuito en HDL es necesario comprobar si el circuito está bien diseñado. La simulación funcional nos permite introducir los valores de las entradas a lo largo del tiempo y ver el resultado que éstos producen en las salidas (o en cualquier señal intermedia) del circuito. Esta simulación supone que las operaciones lógicas se realizan de forma instantánea. Se trabaje con señales binarias, que también pueden agruparse en buses y ver la información como un número binario o en cualquier otra base.

  1. Síntesis (o compilación)

Consiste en convertir las funciones lógicas descritas mediante un HDL en un conjunto de elementos lógicos interconectados que se denomina netlist. Los elementos lógicos serán puertas lógicas en el caso de que la tecnología destina sean ASICs o LUTs si son FPGAs. Como ya comenté antes, la síntesis incluye la optimización de las funciones lógicas. Por ejemplo, si hacemos la operación NOT(NOT A), en lugar de usar dos puertas lógicas encadenadas, no usará ninguna, puesto que NOT(NOT A) = A.

  1. Asignación de pines

En este paso se indica a qué pines están conectadas las señales de entrada y salida del circuito que va dentro de la FPGA. Si no se especifican los pines la herramienta de diseño asignará pines aleatorios. Esta información puede introducirse a través de un fichero de texto o bien mediante una interfaz gráfica. También se aportará información acerca del estándar lógico que se esté usando (es decir, el voltaje asignados a los ceros y los unos: TTL, LVTTL, CMOS, LVCMOS, etc.), si son pines de alta velocidad, etc.

  1. Posicionamiento y rutado

El posicionamiento (placement en inglés) se encarga de elegir exactamente el elemento de la FPGA que se va a utilizar para implementar una LUT. El rutado (routing en inglés) se encarga de conectar los pines y las señales intermedias a las LUTs. Al proceso se le suele englobar en lo que se denomina place and route (que lo veremos como P&R o como PAR).

En las FPGAs las LUTs están agrupadas para disponer de conexiones rápidas entre ellas. Si dos LUTs están en grupos distintos, pero cercano se usará una ruta un poco más lenta y si los grupos están muy separados se usará una ruta de larga distancia, que evidentemente presentará un retardo mayor. Según el fabricante estos grupos reciben nombres distintos (Configurable Logic Block (CLB), Logic Array Block (LAB), etc.) y además el número de LUTs y la topología de interconexión varía. Con esto vemos que el proceso de placement es algo   más complicado de lo que parece a simple vista. Tradicionalmente existía una etapa anterior al placemente que se encargaba de agrupar primero las LUTs de manera que el posicionamiento se aplicaba a los grupos y no a las LUTs individuales. Algunos fabricantes lo llaman mapping y para crear un poco de confusión en algunos casos el mapping también hace placement, y el proceso de P&R sólo hace se encarga del rutado.

  1. Análisis temporal y simulación temporal

Una vez se sabe como quedará cada elemento en la FPGA y cómo estará interconectado las herramientas comprueban que las señales se propagan cumpliendo con la velocidad del reloj del sistema. Si una señal es demasiado lenta, el análisis temporal lo detecta y lo indica al diseñador. Este análisis proporciona los datos necesarios para poder llevar a cabo una simulación que incluya los tiempos que tarda cada señal en recorrer las pistas metálicos (las rutas que llamé antes) y que nos permita comprobar de forma mucho más fiel a la simulación funcional del punto 2 si el circuito está funcionando correctamente.

  1. Configuración del dispositivo

La configuración consiste en enviar los datos contenidos en un fichero llamado bitstream que contiene los valores de configuración de todos los elementos de la FPGA: los valores de cada LUT, el estado de cada conmutador que realiza la interconexión entre LUTs, la configuración de los puertos de entrada y salida, etc. Este bitstream se envía envía mediante un puerto serie directamente a la FPGA, o se envía a una EPROM que queda programada. La FPGA tras el reinicio de la placa estará virgen, puesto que la configuración se almacena en memoria no volátil (SRAM) y tras el apagado del chip se borra; la configuración la lee de la EPROM antes mencionada.

 

Implementación

Aunque sea de mala educación, os voy a dejar con la miel en los labios y vamos a terminar el ejemplo en la siguiente entrada. Que soñéis con circuitos reconfigurables.

 

Enlaces de interés

  • Información sobre la placa DE2-115 [consultado 25/01/2019]
  • DE2-115 User manual (manual de usuario de la placa DE2-115), Terasic Inc. [consultado 25/01/2019]

 

Agradecimientos

Gracias a Terasic Inc. por concederme los permisos para utilizar las fotografías de su web así como las figuras y tablas de la documentación de sus placas.

Dic 22 2018

Hello World. Hello FPGA – Parte I: Toma de contacto con FPGAs

Las FPGAs aparecieron a mediados de los 80 [Trimberger2015] y desde entonces desarrollan un papel relevante en la industria de los semiconductores, junto con microprocesadores, procesadores gráficos y circuitos específicos ASIC. Yo las descubrí en 1996 y no he conseguido desengancharme. Con esta entrada pretendo hacer una introducción a estos dispositivos; tan solo unas pinceladas que sirvan como primera toma de contacto con esta tecnología.

¿Qué es una FPGA?

Los dispositivos FPGA (Field-programmable gate arrays) son circuitos integrados que permiten implementar circuitos digitales. La capacidad de estos dispositivos varía desde cientos de puertas lógicas hasta millones. El diseñador puede configurar la funcionalidad de cientos/millones de bloques lógicos (por ello lo de gate array) así como su interconexión, y esta configuración se puede hacer después de haber fabricado el chip (por ello lo de field-programmable: programable in situ).

Podemos decir que la FPGA está compuesta por una red de memorias que albergan escasos bits. Estas memorias se denominan LUTs (look-up table: tabla de consulta) y permiten implementar funciones lógicas.

Veamos un ejemplo. En la figura se ve una puerta AND con la tabla de verdad que relaciona  sus entradas (a y b) con su salida (c).

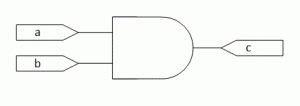
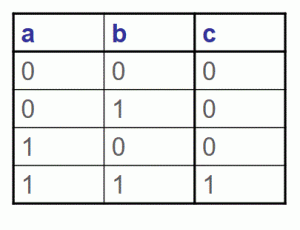Figura. Puerta AND y su tabla de verdad

Las señales a y b son las entradas a la puerta y la señal de salida es c. Se observa como c solamente está activa (‘1’) cuando ambas entradas están a ‘1’.

Otras puertas lógicas de 2 entradas necesitarían tablas similares, es decir, tablas con 4 filas y 3 columnas. De hecho, cualquier función lógica de 2 entradas podría expresarse mediante una tabla del estilo. Estas tablas de verdad son la esencia de las FPGAs, puesto que se implementan directamente como memoria RAM y pasan a ser los bloques lógicos que mencioné antes. De manera que llenando un circuito integrado de pequeñas memorias podemos implementar gran cantidad de funciones lógicas. Nótese que no estoy hablando de usar puertas lógicas, sino memorias. De hecho, y siento ponerme pesado, las puertas lógicas o la combinación de varias puertas se implementan en una FPGA con una memoria. La matriz de puertas (gate array) que forma parte del nombre de las FPGAs es en realidad una matriz de memorias (¿memory array?). De hecho el nombre que utilizaron para la primera FPGA, el dispositivo XC2064 de Xilinx era “matriz de celdas lógicas” (Logic Cell Array, en inglés), pero luego se implantó el termino FPGA introducido por Actel [Trimberger2015].

La tabla del ejemplo anterior se convertiría en la siguiente memoria de 4 bits:

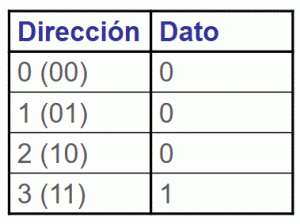Tabla: Interpretación de la tabla de verdad como una memoria

Las señales a y b concatenadas pasan a ser el bus de direcciones y la señal c es el bus de datos. Si a y b valen 1, realmente lo que ocurren es que se leería la posición de la memoria que ocpua la posición 3 (112=3 – leer entrada sobre binario). Ahora tan solo (es un decir) nos quedaría idear un método para poder escribir en muchas LUTs – para disponer de muchas funciones lógicas-, además de disponer de canales de rutado que nos permitieran interconectar dichas LUTs, y también, idear un método para configurar las conectividad de dichos canales. Ahí es ná.

En la figura aparece un esquema de la arquitectura de una FPGA. Los bloques lógicos contienen la funcionalidad y procesan señales que provienen del exterior (señales de entrada y salida (E/S)) o de otros bloques lógicos. Las señales E/S están conectadas a las patillas o pines del chip. Los bloques lógicos producen señales binarias que se conectan a otros bloques lógicos o a las señales de salida. Los canales de rutado se configuran para que se produzca la interconexión entre bloques lógicos y señales de E/S. Obviamos los detalles con la intención únicamente de introducir la tecnología.

Figura: Esquema de arquitectura interna de FPGA (modificación de https://commons.wikimedia.org/wiki/File:Fpga_structure.svg  )

Hay que destacar que el bloque lógico además de la LUT dispone de otros elementos lógicos básicos como puertas lógicas, multiplexores y de un biestable de tipo flip-flop (memoria de un bit), que ya veremos en próximas entradas en las que revisaré la arquitectura de varias FPGAs. Comentar que las FPGAs tienen LUTs con entre 4 y 6 entradas (la LUT de dos entradas era sólo un ejemplo con el que comenzar) dando lugar a funciones lógicas de entre 4 y 6 entradas. Con esto vemos que la FPGA puede implementar circuitos tanto combinacionales como secuenciales -debido a los flip-flops – y, en general, de gran capacidad.

Afortunadamente, el paso de las ecuaciones lógicas a la distribución entre bloques lógicos y su interconexión la realiza una herramienta de ayuda al diseño electrónico, o herramienta EDA (Electronic Design Automation).

Como veis, el proceso difiere bastante del desarrollo software. Para simplificar, algunos fabricantes (como Altera Inc.) utilizan el termino compilación para englobar las fases necesarias para ir de la idea (esquema lógico) a la implementación (FPGA configurada). La diferencia principal es que el tiempo de compilación puede llevar entre varios minutos y varias horas, incluso para diseños relativamente sencillos. El motivo es que hay que tomar muchas más decisiones que las que toma un compilador software.

Un tema espinoso es que la configuración de la FPGA se denomina programación y esto puede dar pie a confusión. Se utiliza programación de igual manera que a la escritura de los datos en una memoria PROM (programable read-only memory: memoria programable de sólo lectura). Esto tiene sentido en el caso de la PROM puesto que lo que se suele almacenar en estas memorias es un programa. Sin embargo, lo que almacenamos en la FPGA es la información lógica de las LUTs y los bits que configuran la interconexión. Yo prefiero decir que las FPGAs se configuran en lugar de que se programan para evitar que se asocie a sistemas software.

En la siguiente figura se ve cómo se distribuyen las LUTs en una FPGA concreta de la familia Cyclone IV de Altera. Cómo se observa, hay un gran número de memorias LUT.  Por ejemplo, dispositivos de la familia Virtex-6 de Xilinx tienen entre 46,000 y 354,000 LUTs. Con esta cantidad de LUTs se pueden hacer muchas cositas.

Figura. Esquema de la distribución de LUTs en dispositivo de la Familia Cyclone IV de Intel FPGA (Altera)

Microprocesador, ASIC y FPGA

Veamos brevemente la diferencia entre estos circuitos integrados:

  • Microprocesador: Circuito integrado que implementa una CPU y los bloques hardware necesarios para la transferencia de datos con la memoria y con los periféricos. Se diseñan para dar soporte a gran cantidad de aplicaciones, por lo que son circuitos costosos y consumen gran cantidad de potencia eléctrica. El punto fuerte del microprocesador es precisamente el hecho de que puedan ejecutar gran cantidad de aplicaciones de forma bastante eficiente. Hay que considerar que los errores en el diseño del microprocesador no se pueden corregir a posteriori al no poderse modificar la estructura del circuito integrado.

Esto último tiene su importancia (mucha). Recordemos el fallo en la división del microprocesador Pentium de Intel descubierto por el profesor Thomas Nicely en 1995 [Cipra1995]. Se “solucionaba” con un parche software que ejecutaba la operación muy lento al ser una emulación software. O más recientemente, las vulnerabilidades tipo Spectre  que afectan a microprocesadores de Intel, IBM y ARM, que de nuevo se solucionan reduciendo el rendimiento del sistema. Todo porque el fallo es hardware y no puede modificarse.

Podríamos decir que el microprocesador realiza continuamente tres tareas básicas:

  1. Lee una instrucción de una memoria (que contiene el programa)
  2. Interpreta la operación
  3. Ejecuta la operación (probablemente leyendo datos de memoria y escribiendo los resultados en memoria)

Tras ejecutar la tarea 3, vuelve a comenzar leyendo la siguiente instrucción (que suele estar en la posición siguiente con respecto a la anterior instrucción leída). El programador trabaja modifica el programa que está en la memoria para realizar cambios en la aplicación. Le es imposible modificar el hardware.

  • ASIC: Estas siglas provienen de Application-Specific Integrated Circuits, es decir, circuito integrado de aplicación específica. Es un circuito integrado que implementa un circuito que ha sido optimizado para una tarea concreta. Está en las antípodas del microprocesador. Al disponer de una arquitectura optimizada se puede optar por reducir al máximo los recursos (número de transistores y consumo de potencia eléctrica) o bien maximizar su potencia de cálculo (sin miramiento en el número de transistores). De nuevo, cualquier fallo en el diseño hardware es fatal suponiendo grandes pérdidas de dinero. Un ejemplo claro de ASIC sería circuitos que implementan procesamiento intensivo en tiempo real: Wi-fi, reconocimiento de imágenes, etc.
  • FPGA: La FPGA es similar al ASIC puesto que permite implementar circuitos optimizados para tareas específicas. La gran ventaja es que si se detectan errores una vez ha salido el producto al mercado, es posible corregirlos, de forma muy similar a como se actualiza el firmware de muchos equipos. En este caso, lo que se modifica es la secuencia de configuración de la FPGA que ésta carga siempre tras el arranque. La pega que tienen estos dispositivos es que el coste a pagar para conseguir la capacidad de reconfiguración es que se utilizan muchos recursos. La FPGA es más lenta que el ASIC y consume más que este. Para determinadas aplicaciones, es mucho más rápida que un microprocesador y consume mucho menos.

Si nos fijamos en la velocidad de los relojes que consiguen las FPGAs, hace una década rondaban los 200 MHz y en la actualidad rondan los 400 MHz (los fabricantes os dirán que es mucho más; es fácil hablar, lo difícil es diseñar sistemas). Con estas velocidades de reloj podríamos pensar que una FPGA no puede competir con una CPU que corre a varios Gigahertzios. La clave está en el paralelismo y en la posibilidad de adecuar de forma óptima (según el arte del diseñador) los diseños a una aplicación específica. Supongamos un reloj de 200 Mhz y una aplicación que debe realizar 10 multiplicaciones de enteros de 16 bits por cada dato de entrada. Si el algoritmo permite realizar las 10 multiplicaciones en paralelo, y si la FPGA permite que se implementen 10 multiplicadores, se podrán realizar 10x200e6 = 2e9 multiplicaciones por segundo. Pronto os hablaré de algún diseño propio en el que se consigue ir 10000 veces más rápido que un microprocesador i7.

Termino diciendo que cada tecnología tiene su nicho, su punto óptimo. Hay que considerar que la FPGA requiere tiempos de desarrollo altos y que no siempre es posible paralelizar.

Aquí descanso con la intención de continuar la entrada con varias partes. En la siguiente entrada veremos las etapas del flujo de diseño con FPGA a través de un sencillo ejemplo.

Mientras tanto os dejo algunos enlaces de interés:

“FPGA for Dummies”: https://plan.seek.intel.com/PSG_WW_NC_LPCD_FR_2018_FPGAforDummiesbook

Intel FPGAs: https://www.intel.com/content/www/us/en/products/programmable/fpga.html

Xilinx: https://www.xilinx.com/products/silicon-devices/fpga.html

Lattice: https://www.latticesemi.com/Products#_D5A173024E414501B36997F26E842A31

 

Referencias

[Trimberger2015] “Three Ages of FPGAs: A Retrospective on the First Thirty Years of FPGA Technology”, Proceedings of the IEEE, 2015

[Cipra1995] “How Number Theory Got the Best of the Pentium Chip “, Barry Cipra, Science, 1995 [pdf]

 

 

Nov 30 2018

Torres Quevedo y el primer ordenador de la historia

Estoy en plena fase de lectura intensiva sobre las invenciones de Leonardo Torres Quevedo, y, aunque sea algo prematuro, me gustaría ir compartiendo mis hallazgos, sobre todo los relacionados con el mundo de la computación. Por otra parte, soy español y me paso la vida hablando de pioneros de la electrónica y la informática nacidos o que desarrollan su actividad en EE.UU., Japón, etc., y creo que no está mal de vez en cuando mirar qué sale de mi propia tierra. Sin ánimo de quitar mérito a nadie, hay una clara americanización de la historia de la computación, y para determinados temas hay que hacer el esfuerzo de ir a buscar la información y no que sea ella la que te encuentre.

El motivo por el que empiezo esta búsqueda es mi interés en una faceta de la computación que el público/usuario general asume de forma errónea: los ordenadores (léase sistemas digitales) cometen errores matemáticos en sus cálculos. El problema fundamental es que el número de dígitos que utiliza un ordenador para almacenar un número es finito, por lo que no todos los valores numéricos pueden representarse de forma correcta, y esto hace que los resultados de las operaciones conlleven errores, que a su vez se propagan si éstos son usados por otras operaciones. Y es aquí donde enlazo con Torres Quevedo, puesto que leí en algún sitio que fue pionero al proponer a principios de siglo XX uno de los formatos aritméticos más utilizado por los ordenadores hoy en día. “Pero esa es otra historia y será contada en otra ocasión”, no muy lejana.

El hecho en el que me centro esta vez es impresionante: Torres Quevedo definió la arquitectura de un ordenador y de sus componentes basado en sistemas electromecánicos, varias decadas antes de que se crease el primer ordenador. En 1920 creó un sistema capaz de ejecutar comandos desde un teclado y aún está por ver si la implementación del mismo se basa en los mismos fundamentos de sus escritos, con lo cual habría construido el primer ordenador de la historia.

Mi búsqueda en las bases de datos del IEEE y la ACM arroja pocos artículos: [Randell82][Yuste2005][Yuste2008]… Hay varios libros en español sobre el tema, algunos descatalogados y otros que no profundizan demasiado o que tienen información incompleta. El propio Randell trata los inventos digitales de Torres Quevedo en su libro “Origins of Digital Computers” (Springer, 1982), pero no he tenido la oportunidad de leerlo. Destaca el libro de Alfonso Hernando González el cual, como comento más abajo, está disponible online. El artículo de Randel [Randell82] me ha servido para andar este camino, además de los trabajos de Hernando [Hernando1991] y los artículos de Yuste y compañía.

Comencemos:

Leonardo Torres Quevedo nació el 28 de diciembre de 1852 en Santa Cruz (Cantabria, España). Estudió Ingeniería de Caminos, Canales y Puertos y su carrera profesional estuvo plagada de logros. Trabajó en diversas disciplinas tales como la aeronáutica, la automática, las telecomunicaciones y la mecánica. Sus inventos van desde las máquinas de cálculo analógicas, pasando por sistemas de control remoto por radio, hasta el diseño y fabricación de aviones semi-rígidos que se utilizaron en la primera guerra mundial. Su “Spanish Aero Car” aún sigue en funcionamiento en las cataratas del Niagara. Y también fue muy prolífico en el diseño de dispositivos de cálculo y en el de autómatas.

File:El eminente sabio español Leonardo Torres Quevedo, de Franzen.jpg

El eminente sabio español Leonardo Torres Quevedo (wikipedia)

Es famoso su Ajedrecista, el cual se considera el primer autómata de ajedrez, que realizaba el final de rey con torre contra rey, jugando – y ganando—contra un oponente humano. Se puede consultar su diseño en la publicación Le Nature de 1914 [Vigneron1914].

File:El Ajedrecista de Leonardo Torres Quevedo 02.jpg

El Ajedrecista de Leonardo Torres Quevedo (wikipedia)

Una de sus principales motivaciones era explorar las posibilidades que ofrecían las técnicas electromecánicas  y poner a prueba los límites de las máquinas. En su trabajo Ensayos sobre automática [Torres1914] nos habla de la obra de Babbage, el cual propuso por primera vez la construcción de máquinas capaces, no solo de realizar operaciones matemáticas, sino de ejecutar un programa. La máquina analítica de Babbage fue concebida para ser puramente mecánica, permitía almacenar datos (lo que serían los registros de la CPU), disponía de operadores aritméticos, tal como la suma, multiplicación y división (el equivalente a la unidad aritmético lógica (ALU)) y sus programas permitían bucles y toma de decisiones (saltos condicionales). En este último apartado, el de la programación, destacó Ada Lovelace como la primera programadora de la historia, porque, aunque ni Babbage ni ella llegaron a ver la máquina construida, escribió los primeros algoritmos que podía ser ejecutados por una máquina motivada por los escritos de Babbage. La máquina analítica nunca llegó a construirse y Torres Quevedo parte de ella para realizar una implementación describir cómo se podría implementar mediante sistemas electromecánicos. En este escrito se enfrenta al diseño de una máquina capaz de realizar la operación ax(y-z)2 para unos valores de entrada de las variables. La máquina disponía de los mismos bloques que la máquina de Babbage, pero adaptados a la tecnología electromecánica del momento: bloque aritmético (ALU), bloque de almacenamiento temporal (registros) y programa de solo lectura (ROM) que permitía realizar saltos condicionales.

Automáta para el cálculo de ax(y-z)^2 (“Ensayos sobre automática” 1914)

Tras este esfuerzo intelectual, construye varios sistemas digitales prototipos y es en 1920 cuando presenta en París el Aritmómetro. Esta invención, permitía escribir qué operación aritmética se quería realizar mediante una máquina de escribir y la máquina ejecutaba un programa acorde a la operación elegida. Supuestamente, internamente disponía de un programa de solo lectura que controlaba los operadores aritméticos, la memoria temporal, etc. Si esto es cierto, estaríamos antes un ordenador que ejecutaba un programa (probablemente almacenado en un tambor, tal como describe él mismo). Para cambiar el programa era necesario construir un nuevo tambor e introducirlo en la máquina [Hernando1991]. De ahí a las tarjetas perforadas  había un paso.

Hay que resaltar que Torres Quevedo no estaba considerando el uso de grandes memorias de almacenamiento, lo que sería la RAM, si no tan solo, el almacenamiento de valores temporales o de resultados finales de las operaciones – más en la línea de lo que son los registros de la CPU. Es probable, que la complejidad de almacenar y direccionar grandes cantidades de datos estuviese fuera del alcance de la tecnología de la época.

En [Hernando1991] se indica que la obra Ensayos sobre automática es “uno de los textos cumbres de la historia de la informática”. Hernando resalta que Torres Quevedo destaca la importancia de las máquinas digitales, que permiten controlar sistemas reaccionando a las condiciones del entorno o de los propios datos calculados. Claramente un comentario visionario. También  propone la creación de una rama específica de estudio llamada Automática, la cual, de haberse desarrollado en ese momento, habría adelantado en el tiempo  facetas de la electrónica y la informática que tardaron en aparecer varias décadas. También, el inventor hace énfasis en que los autómatas no sólo deben centrarse en realizar cálculos matemáticos de forma automática, sino que debían abordar cualquier tipo de problema, de nuevo adelantándose a las propuestas de Turing y Von Neumann. Hernando realizó su Tesis Doctoral sobre la obra de Torres Quevedo y ha puesto a disposición su libro del año 2000 basado en la misma en su blog.

Sin embargo, parece ser que el impacto de las teorías e inventos sobre computación ha sido nulo en el desarrollo de la informática, debido a su falta de difusión [Hernando1991]. De no haber sido así, la historia de la informática habría seguido otros derroteros, apareciendo el ordenador mucho antes. Los logros de Leonardo Torres Quevedo son anteriores a Turing (que nació en 1912) y varias décadas anteriores a los ordenadores de los 40 en los que se basó la informática moderna.

Con esta entrada tan solo quería difundir la relación de Torres Quevedo con la historia de la informática sin entrar en detalles sobre el funcionamiento de sus inventos. Espero disponer de tiempo para poder analizar los diseños de este gran científico e inventor y poder contarlos con detalle en el futuro.

Queda pendiente poder acceder a más información sobre el Aritmómetro para confirmar si realmente se trata del primero ordenador de la historia.

Enlaces de interés

The Babbage Engine, Computer History Museum (consultado 30/11/2018)

Biografía de Leonardo Torres Quevedo, ITEFI-CSIC (consultado 30/11/2018)

Actas del Simposio “Leonardo Torres Quevedo: su vida, su tiempo, su obra”, 1987, 1991 y 1995 (consultado 30/11/2018)

Blog de Alfonso Hernando González (consultado 30/11/2018)

Referencias

[Randell1982] “From Analytical Engine to Electronic Digital Computer: The Contributions of Ledgate, Torres, and Bush”, Brian Randell, Annals of the History of Computing, IEEE, 1982

[Vigneron1914] «Les automates», H. vigneron Le Nature, 1914 (El ajedrecista)

[Torres1914] “Ensayos sobre Automática. Su definición. Extensión teórica”, L. Torres  Quevedo, Revista de la Real Academia de las Ciencias, 1914 [PDF]

[Hernando1991] “Torres Quevedo como precursor de la informática moderna”, A. Hernando González, Actas del Simposio Leonardo Torres Quevedo: su vida, su tiempo, su obra, 1991 [PDF]

[Yuste2005] “Scanning Our Past from Madrid: Leonardo Torres Quevedo”, A.P. Yuste, M.S. Palma, Proceedings IEEE, 2005

[Yuste2008] “Early Developments of Wireless Remote Control: The Telekino of Torres-Quevedo”, A.P. Yuste, Proceedings IEEE, 2008

Nov 21 2018

Total recall: “6502: semilla de la revolución digital” (2017)

El microprocesador 6502 era magia hecha de bits. Los creadores de este microchip son verdaderos héroes digitales que consiguieron lo imposible: crear un microprocesador de bajo coste en 1975 que moldeó la industria de la electrónica. Este dispositivo se usó en máquinas legendarias: Atari VCS 2600, Apple II, Commodore 64, Nintendo Famicon, etc. Un GIF animado vale más que mil palabras:

(a veces la animación falla, prueba aquí)

En 2017 impartí dos charlas sobre este tema. Primero, en abril de 2017, tuve la oportunidad de homenajear a este pequeño y maravilloso micro con una presentación que hice en el evento de computación clásica RetroMadrid. Posteriormente, extendí un poco la charla y la impartí como parte del evento de divulgación científica organizado por la Comunidad de Madrid, (Semana de la Ciencia 2017, noviembre de 2017). Disfruté enormemente el proceso de conectar los numerosos puntos que perfilan una historia fascinante y única. También, recibí gran cantidad de comentarios interesantes de la audiencia, a la que estoy muy agradecido. Por cierto, la segunda charla tiene un final alternatico… en varios sentidos.

Los contenidos de la charla son:

  • Repaso corto (y bastante informal) de circuitos digitales y circuitos integrados
  • Chuck Peddle y Motorola: ¿Competimos con Intel?
  • Chuck Peddle y MOS Technology: ¿Construimos un microprocesador de bajo coste?
    • El equipo del 650x
    • Diseño del chipset 650x
    • Vendiendo el micro
    • Motorola ataca de nuevo
  • 6502 y Commodore
  • 6502 y… Commodores, Atari, Apple, ARM, Nintendo, etc., etc.
  • El 6502 hoy en día
    • Libros, microchips y kits
    • FPGAs
    • Visual6502
    • 6502 y la Neurociencia
  • El público se vuelve loco

Tengo que destacar que mis charlas están basadas en libros y documentos en los que hay información que posteriormente he comprobado que no era totalmente objetiva, así que la historia que cuento tiene ciertas imprecisiones que deberían ser investigadas en más detalle. Espero tener tiempo para poder hacerlo.  Desde que me di cuenta de esto, intento ser cuidadoso con las fuentes que uso y siempre intento desarrollar mi propia versión de la historia, dejando claro qué son hechos y qué es una opinión (mía o de otra persona).  [Este tema lo desarrollo un poco en mi charla sobre la invención del microprocesador]

Resumientdo, no importa si eres un nostálgico de Zilog, Motorola, Texas Instruments, etc., la historia del 6502 debe ser contada, porque este microprocesador es un elemento esencial para comprender la creación del PC y el nacimiento de la industria del videojuego.

A destacar:

  • El proceso microelectrónico era manual. Era necesario dibujar a mano las diferentes capas del microchip. Esto también ocurrió así en el desarrollo del Intel 4004.
  • Un tipo llamado Steve Wozniak compró varios chips de la primera tanda de 6502 que se vendió y construyó  el ordenador Apple I.  Este microprocesador hizo posible construir ordenador a un precio asequible.
  • Dos de los tres ordenadores personales más vendidos, lo cuales animaron a IBM a entrar en el negocio del ordenador personal, tenían como cerebros el 6502:  Apple II (6502), Commodore PET (6502) y Tandy TRS-80 (Z80).
  • La creación del 6502 y el hecho de que una compañía mediana (Western Design Center) fuese capaz de diseñar y fabricar microchips sirvió de inspiración para que ingenieros de Acorn desarrollasen sus propios microprocesadores, con el resultado de que años más tarde nació ARM.

 

Referencias

6502.org: Página sobre el 6502 con gran cantidad de información.
The Visual 6502 project: ¿Queréis ver la actividad de los transistores mientras se ejecuta código en ensamblador? Este es el sitio adecuado.
Apple][ history website: El sitio de referencia para aprender sobre el Apple ][
Commodore: a company on the edge: Fantástico libro sobre los primeros pasos en el mundo de la informática de Commodore Bussiness Machines. Se describe de forma sublime la creación del chip 6502.

Charlas

  • El microprocesador 6502 y su impacto en la revolución digital (Spanish), RetroMadrid 2017, [slides]
  • Historia del microprocesador 6502: semilla del PC y de la industria de los videojuegos (Spanish), Semana de la Ciencia 2017 [slides (with alternative ending 🙂 )]

Oct 16 2018

Sinistar: el arcade de la eterna juventud

No hay nada como encontrar un ejemplo divertido (esto siempre es cuestionable) para apoyarse a la hora explicar uno de tantos áridos conceptos que pueblan la electrónica digital, la computación y el procesamiento de señal. Hace tiempo me topé con un vídeo fantástico publicado por la revista IEEE Spectrum (Five Infamous Arcade-Game Glitches), en el que hablaban de fallos de programación (glitches) en juegos de máquinas recreativas: Asteroids (Atari), Donkey Kong (Nintendo), Sinistar (Williams Electronics), Ms. Pacman (Midway) y Centipede (Atari) .

Me llamó la atención el glitch del juego Sinistar, que me venía de perlas para explicar la aritmética en complemento a 2, fundamental en el mundo de los sistemas digitales. En este juego existía la posibilidad de pasar de tener 1 única vida a disponer de 255. Todo esto debido a un despiste de programación y al funcionamiento de la aritmética binaria (en este caso de 8 bits). Por cierto, matizar que lo que voy a contar es bastante simple, pero divertido.

Primero os explico muy por encima un par de conceptos sobre binario que si ya tenéis experiencia podéis ir directos al meollo pulsando aquí.

Continue reading

Bitnami